Формула Ньютона-Лейбница

Формула Ньютона-Лейбница относится к математическому анализу и является основной формулой интегрального исчисления!

Ранее, когда мы рассматривали Формулу бинома Ньютона, мы сказали что Исааку Ньютону принадлежит роль "Отца современной математики". Ньютон вместе с Лейбницем, Огюстеном Коши, Кантором, Леонардом Эйлером и другими заложили основы современного дифференциального и интегрального исчисления, хотя строгое и стройное построение математического анализа возникло несколько позже.

Благодаря формуле Ньютона-Лейбница устанавливается связь между определенным и неопределенным интегралом. А именно:

Чтобы решить определенный интеграл, надо сначала вычислить неопределенный интеграл (или найти первообразную), а затем вычислить определенный интеграл, подставив первообразную подынтегральной функции в формулу Ньютона-Лейбница:

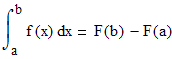
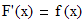
Здесь F(x) - первообразная для функции f(x)! Таким образом, чтобы применить формулу Ньютона-Лейбница, надо вычислить значение первообразной при верхнем пределе интегрирования B, при нижнем пределе интегрирования - A, а затем взять их разность F(b)-F(a). Вначале мы рассмотрим доказательство данной формулы, а затем приведем Примеры решения интегралов по основной формуле интегрального и дифференциального исчисления.

21.Правила Лопіталя розкриття невизначеностей

Теорема 3.10. (І правило Лопіталя). Якщо:

1) функці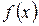ї і 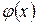диференційовні на інтервалі 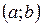, 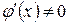для всіх ;

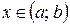2) ;

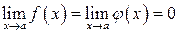3) існує скінченна або нескінченна границя ,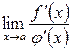

то існує границя 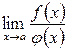, причому має місце рівність:

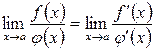. (3.21)

Доведення. Довизначимо функці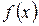ї і 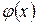в точці 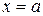так, щоб вони стали неперервними, тобто покладемо 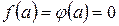. Тепер 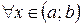ці функції на відрізку 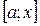, (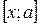) задовольняють умови теореми Коші. Тому існує точка с, 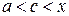, (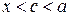) така, що

.

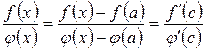Оскільки 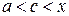, (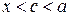) то . Перейшовши в останній рівності до границі, за умови 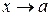, отримаємо

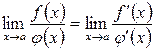що і потрібно було довести.

Запам’ятай добре! Доведену теорему зазвичай називають правилом Лопіталя розкриття невизначеності 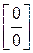за умови .

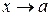Аналогічні теореми мають місце для розкриття невизначеності 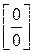у випадку односторонніх границь при , .

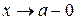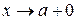Наслідок 2. Якщо похідн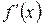і і 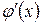задовольняють ті самі вимоги, що і функці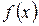ї і 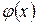, то правило Лопіталя можна застосувати повторно. При цьому отримаємо

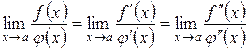. (3.22)

І взагалі, правило Лопіталя при виконанні умов теореми можна застосовувати багаторазово.

Наслідок 3. Якщо в теоремі замінити умову 2) на наведену нижче

2) 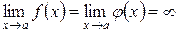, або 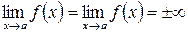, то формула (3.21) також має місце.

В цьому випадку правило Лопіталя застосовується для розкриття невизначеності типу 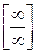(ІІ правило Лопіталя).

Date: 2015-09-18; view: 538; Нарушение авторских прав