Формули Тейлора та Маклорена

Для функції, яка диференційовна 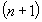раз включно в околі точки 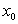має місце формула Тейлор а:

, .
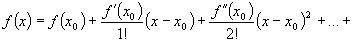
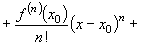
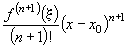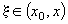Останній доданок у формулі Тейлора

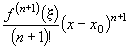
називають залишковим членом у формі Лагранжа, і якщо 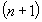похідна обмежена, то він прямує до нуля при .
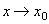При 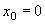ця формула набуває вигляду:

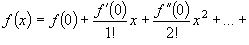
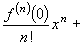
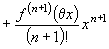, де .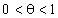
Її називають формулою Маклорена.

У точці 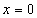сама функція 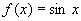і похідні парних порядків (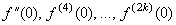) дорівнюють нулю, а всі похідні непарних порядків дорівнють .
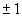Отже,
.
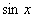
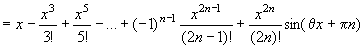Аналогічно записують формулу Маклорена для функції 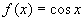, а саме

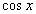
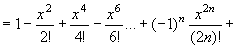
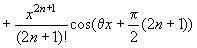
За допомогою формул Тейлора і Маклорена складні функції з великою точністю замінюють многочленами, що полегшує обчислення.

23 Ознаки монотонності функції.

· (Критерій монотонності функції, що має похідну на інтервалі) Нехай функція неперервна на (A, b), і має в кожній точці 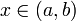похідну f '(x). Тоді

f зростає на (A, b) тоді і тільки тоді, коли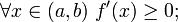

f убуває на (A, b) тоді і тільки тоді, коли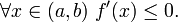

· (Достатня умова суворої монотонності функції, що має похідну на інтервалі) Нехай функція неперервна на (A, b), і має в кожній точці 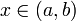похідну f '(x). Тоді

якщо 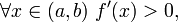то f строго зростає на (A, b);

якщо 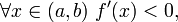то f строго убуває на (A, b).

Зворотне, взагалі кажучи, невірно. Похідна строго монотонною функції може звертатися в нуль. Однак, безліч точок, де похідна не дорівнює нулю, має бути щільно на інтервалі (A, b). Точніше має місце

· (Критерій суворої монотонності функції, що має похідну на інтервалі) Нехай 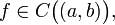і всюди на інтервалі визначена похідна f '(x). Тоді f строго зростає на інтервалі (A, b) тоді і тільки тоді, коли виконані наступні дві умови:

1.

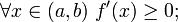
2.

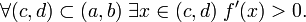
Аналогічно, f строго убуває на інтервалі (A, b) тоді і тільки тоді, коли виконані наступні дві умови:

1.

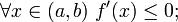
2.

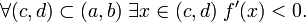
24. Екстремум функції.

Точка х₀ називається точкою локального максимуму функції 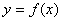, якщо для будь-яких досить малих 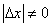виконується нерівність

.

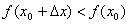Точка х₀ називається точкою локального мінімуму функції 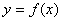, якщо для будь-яких досить малих 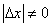виконується нерівність

.

Точки максимуму і мінімуму називаються точками екстремуму функції 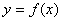, а значення функції в екстремальних точках – її екстремальними значеннями.

Необхідну ознаку локального екстремуму дає така теорема:

Теорема 1. Якщо функція 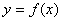має в точці х₀ локальний екстремум, то 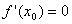або , або 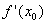не існує.

Проте виявляється, що цього недостатньо, бо може 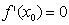, а функція 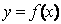в цій точці екстремуму не має.

Точки, в яких функція 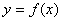визначена та неперервна, і в цих точках 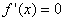або не існує, називаються критичними для функції.

Проте не в кожній критичній точці функція 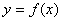має екстремум. Тому потрібні достатні ознаки існування екстремуму для функції f. Їх дають такі теореми:

Теорема 2.

Нехай функція 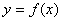неперервна в деякому інтервалі, який містить критичну точку х₀, і диференційована у всіх точках цього інтервалу (за винятком, можливо, самої точки х₀).

Якщо для х<х₀ 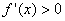, а для х₀<x 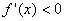, то для х=х₀ функція 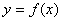має максимум.

Якщо для х<х₀ 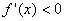, а для х₀<x 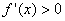, то для х=х₀ функція 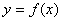має мінімум.

Теорема 3.

Нехай функція 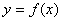два рази диференційована в околі точки х₀ і 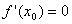. Тоді в точці х=х₀ функція має локальний максимум, якщо 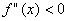, і локальний мінімум, якщо .

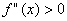Якщо ж 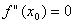, то точка х=х₀ може й не бути точкою екстремуму.

Звідси випливає такий план знаходження екстремальних точок:

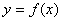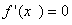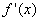1. знаходять критичні точки функції , тобто точки, в яких , або не існує;2. знаходять другу похідну 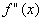і обчислюють значення другої похідної в цих точках.

Якщо значення другої похідної в критичній точці від’ємне, то така точка є точкою максимуму, а якщо значення другої похідної додатне, то точка є точкою мінімуму.

Якщо 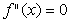в критичній точці, то нічого конкретного сказати не можна, бо в цій точці може бути екстремум, а може й не бути.

Розглянемо тепер дослідження функції на екстремум на конкретних прикладах.

Приклад 1.

Дослідити на екстремум функцію

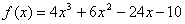
Розв’язання.

Функція 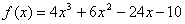визначена і диференційована на R. Знайдемо її похідну:

.

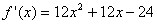Знайдемо нулі похідної:

х²+х-2=0, х₁=-2 х₂=1.

Отже, функція f має дві критичні точки х₁=-2,х₂=1.

Оскільки похідна є квадратним тричленом з додатним коефіцієнтом при х², то на інтервалах 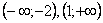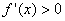, а на інтервалі (-2;1) .

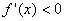Похідна неперервна на R і при переході через критичну точку змінює знак на протилежний.

Оскільки при переході через критичну точку х=-2 похідна змінює знак з плюса на мінус, то в цій точці функція має локальний максимум.

.

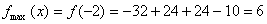При переході через точку х=1 похідна змінює знак з мінуса на плюс. Тому в цій точці функція f має локальний мінімум.

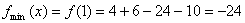
25. Умова опуклості або угнутості кривої.

Друга похідна. Опукла й увігнута функція.

Достатня умова ввігнутості (опуклості) функції.

Точка перегину.

Друга похідна. Якщо похідна f ' (x) функції f (x) диференційовна в точці (x₀), то її похідна називається другою похідною функції f (x) у точці (x₀), і позначається f '' (x₀).

Функція f (x) називається опуклою на інтервалі (a, b), якщо її графік на цьому інтервалі лежить нижче дотичної, проведеної до кривої y = f (x) у будь-якій точці (x₀, f (x₀)), x₀ 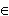(a, b).

Функція f (x) називається ввігнутою на інтервалі (a, b), якщо її графік на цьому інтервалі лежить вище дотичної, проведеної до кривої y = f (x) у будь-якій точці (x₀, f (x₀)), x₀ 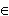(a, b).

Достатня умова ввігнутості (опуклості) функції.

Нехай функція f (x) двічі диференційовна (має другу похідну) на інтервалі (a, b), тоді:

якщо f '' (x) > 0 для будь-якого x 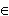(a, b), то функція f (x) є ввігнутою на інтервалі (a, b);

якщо f '' (x) < 0 для будь-якого x 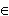(a, b), то функція f (x) є опуклою на інтервалі (a, b).

Точка, при переході через яку функція міняє опуклість на ввігнутість або навпаки, називається точкою перегину. Звідси треба, що якщо в точці перегину x₀ існує друга похідна f '' (x₀), те f '' (x₀) = 0.

П р и м е р.

Розглянемо графік функції y = x3 : 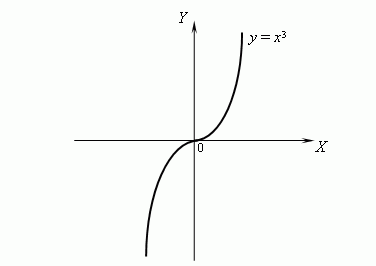Ця функція є ввігнутою при x > 0 й опуклої при x < 0. Справді, y'' = 6x, але 6x > 0 при x > 0 й 6x < 0 при x < 0, отже, y'' > 0 при x > 0 й y'' < 0 при x < 0, звідки треба, що функція y = x3 є ввігнутою при x > 0 й опуклої при x < 0. Тоді x = 0 є точкою перегину функції y = x3.

26. Асимптоти кривої. Побудова графіка функції.

Date: 2015-09-18; view: 552; Нарушение авторских прав