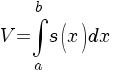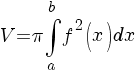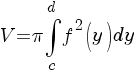Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Асимптоти кривих
|
|
Нехай крива задана рівнянням, де є неперервною функцією на відрізку. Тоді задана крива всіма своїми точками знаходитиметься в замкненому прямокутнику, де є найбільше значення функції на відрізку.
Якщо функція задана на нескінченному проміжку або у випадку, коли проміжок скінчений, але містить точки розриву другого роду заданої функції, то криву не завжди можна розмістити в прямокутнику. Тоді крива або окремі її вітки йдуть в нескінченність. При цьому може трапитися так, що крива на нескінченності, "розпрямляючись”, наближається до деякої прямої лінії (рис.6.21).
Означення. Пряма лінія називається асимптотою кривої, якщо відстань точки кривої до прямої прямує до нуля, коли точка по кривій рухається в нескінченність, тобто
Загальна схема дослідження функції та побудова її графіка
Наочне уявлення про хід зміни функції дає її графік, тому його побудова повинна бути заключним етапом дослідження функції, в якому мають використовуватися всі результати її дослідження. Для зручності дослідження функції рекомендуємо вести в деякій певній послідовності.
1. Знайти область існування функції. Це дає змогу визначити ті точки осі абсцис, над якими пройде чи не пройде графік функції.
2. Знайти точки перетину графіка з координатними осями. Для цього треба розв'язати дві системи рівнянь:
Перша система дає точки перетину з віссю, друга – з віссю.
3. Дослідити функцію на періодичність, парність і непарність. Розв'язання цього питання полегшить побудову графіка в тому розумінні, що її доведеться виконувати не в усій області існування функції, а тільки в її частині. Так, якщо - періодична функція з періодом, то графік достатньо побудувати на відрізку числової осі, довжина якого дорівнює, а потім цю частину графіка повторити на кожному відрізку довжини. Якщо функція парна, то графік функції симетричний відносно осі, якщо не тільки при, а потім симетрично відобразити і на від'ємні.
4. Знайти точки розриву функції та дослідити їх характер. Це допоможе встановити вигляд графіка функції поблизу цих точок.
5. Знайти значення функції на кінцях відрізків, де визначена функція. Якщо область існування функції є інтервал (півінтервал) або кілька інтервалів (півінтервалів), то треба знайти граничне значення функції, коли наближається до одного з кінців розглядуваних проміжків.
6. Визначити інтервали монотонності функції.
7. Знайти екстремальні точки і побудувати їх на площині.
8. Знайти інтервали вгнутості та опуклості кривої, яка є графіком функції.
9. Знайти точки перетину і побудувати їх на площині.
10. Знайти асимптоти графіка функції.
11. Побудувати графік функції.
27. Застосування правил Лопіталя до обчислення границь функцій.
Пра́вило Лопіта́ля — у математичному аналізі — метод знаходження границь функції, розкриття невизначеностей вигляду 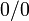 і
і 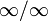 . Теорема, що обґрунтовує метод, стверджує що за деяких умов границя від частки функцій дорівнює границі частки їхніх похідних.
. Теорема, що обґрунтовує метод, стверджує що за деяких умов границя від частки функцій дорівнює границі частки їхніх похідних.
Тема 3. ДИФЕРЕНЦІАЛЬНЕ ЧИСЛЕННЯ ФУНКЦІЇ ОДНІЄЇ ЗМІННОЇ
3.6. Правила Лопіталя розкриття невизначеностей (L'Hospital rule)
Теорема 3.10. (І правило Лопіталя). Якщо:
1) функції 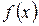 і
і 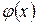 диференційовні на інтервалі
диференційовні на інтервалі 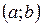 ,
, 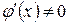 для всіх
для всіх 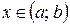 ;
;
2) 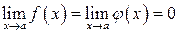 ;
;
3) існує скінченна або нескінченна границя 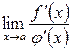 ,
,
то існує границя 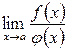 , причому має місце рівність:
, причому має місце рівність:
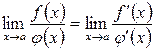 . (3.21)
. (3.21)
Доведення. Довизначимо функції 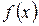 і
і 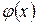 в точці
в точці 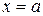 так, щоб вони стали неперервними, тобто покладемо
так, щоб вони стали неперервними, тобто покладемо 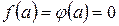 . Тепер
. Тепер 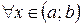 ці функції на відрізку
ці функції на відрізку 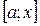 , (
, (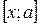 ) задовольняють умови теореми Коші. Тому існує точка с,
) задовольняють умови теореми Коші. Тому існує точка с, 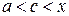 , (
, (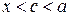 ) така, що
) така, що
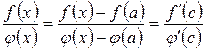 .
.
Оскільки 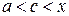 , (
, (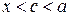 ) то
) то  . Перейшовши в останній рівності до границі, за умови
. Перейшовши в останній рівності до границі, за умови 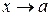 , отримаємо
, отримаємо
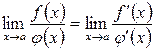 що і потрібно було довести.
що і потрібно було довести.
Запам’ятай добре! Доведену теорему зазвичай називають правилом Лопіталя розкриття невизначеності 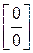 за умови
за умови 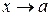 .
.
Аналогічні теореми мають місце для розкриття невизначеності 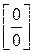 у випадку односторонніх границь при
у випадку односторонніх границь при 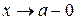 ,
, 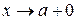 .
.
Приклад 3.24. Обчислити границю 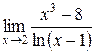 .
.
Розв’язання. Ми маємо невизначеність типу 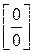 . Функції
. Функції 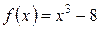 і
і 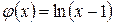 задовольняють умови теореми в деякому околі точки
задовольняють умови теореми в деякому околі точки 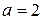 . Застосуємо правило Лопіталя:
. Застосуємо правило Лопіталя:
 .
.
Наслідок 1. Теорема Лопіталя справедлива також при 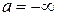 , при
, при 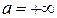 і при
і при 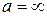 .
.
Приклад 3.25. Обчислити границю 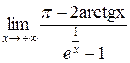 .
.
Розв’язання. Маємо невизначеність типу 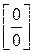 . Застосуємо правило Лопіталя:
. Застосуємо правило Лопіталя:
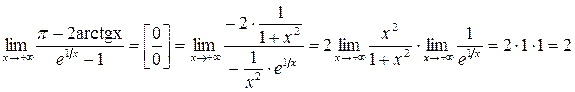 .
.
Наслідок 2. Якщо похідні 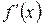 і
і 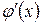 задовольняють ті самі вимоги, що і функції
задовольняють ті самі вимоги, що і функції 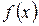 і
і 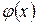 , то правило Лопіталя можна застосувати повторно. При цьому отримаємо
, то правило Лопіталя можна застосувати повторно. При цьому отримаємо
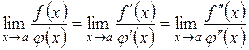 . (3.22)
. (3.22)
І взагалі, правило Лопіталя при виконанні умов теореми можна застосовувати багаторазово.
Приклад 3.26. Обчислити границю 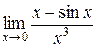 .
.
Розв’язання. Дана границя дозволяє використовувати формулу (3.21) багаторазово, дійсно:
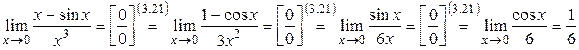 .
.
Наслідок 3. Якщо в теоремі замінити умову 2) на наведену нижче
2) 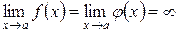 , або
, або 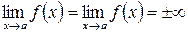 , то формула (3.21) також має місце.
, то формула (3.21) також має місце.
В цьому випадку правило Лопіталя застосовується для розкриття невизначеності типу 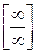 (ІІ правило Лопіталя).
(ІІ правило Лопіталя).
Приклад 3.27. Якщо 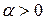 , то
, то
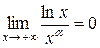 ,
,
тобто довільний додатний степінь x зростає швидше, ніж 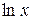 при
при 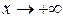 .
.
Розв’язування. Дійсно, застосувавши ІІ правило Лопіталя, отримаємо
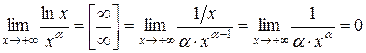 .
.
Приклад 3.28. Якщо 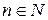 ,
, 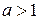 то
то
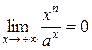 ,
,
тобто, при 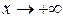 степенева функція
степенева функція 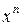 зростає повільніше, ніж показникова функція
зростає повільніше, ніж показникова функція 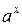 ,
, 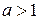 .
.
Розв’язування. Дійсно, застосувавши правило Лопіталя розкриття невизначеності 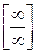 n раз, отримаємо:
n раз, отримаємо:
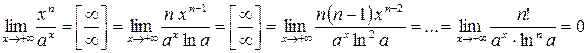 .
.
Зазначимо, що формули (3.21), (3.22) мають місце лише тоді, коли існує скінченна або нескінченна границя 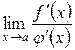 . Але буває і так, що границя
. Але буває і так, що границя 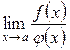 існує, у випадку коли границя
існує, у випадку коли границя 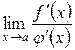 не існує.
не існує.
Приклад 3.29. 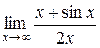 існує і дорівнює
існує і дорівнює 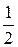 .
.
Розв’язання. Дійсно
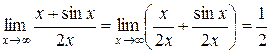 .
.
Але відношення похідних 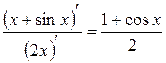 не має границі при
не має границі при 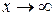 .
.
Після певних перетворень правило Лопіталя може бути застосовано також до розкриття інших невизначеностей, таких як: 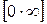 ,
, 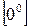 ,
, 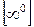 ,
, 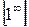 ,
, 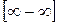 .
.
Так, границі невизначеностей типів 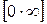 та
та 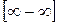 доцільно звести до виду
доцільно звести до виду 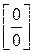 або
або 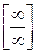 .
.
Приклад 3.30. Обчислити границю  .
.
Розв’язання. Маємо невизначеність типу 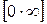 . Приведемо цю невизначеність до виду
. Приведемо цю невизначеність до виду 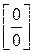 і застосуємо правило Лопіталя.
і застосуємо правило Лопіталя.
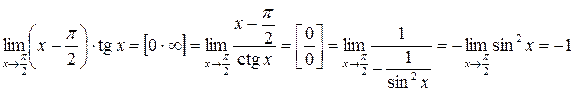 .
.
Приклад 3.31. Обчислити границю 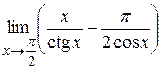 .
.
Розв’язання. Маємо невизначеність типу 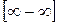 . Спочатку зведемо дроби до спільного знаменника.
. Спочатку зведемо дроби до спільного знаменника.
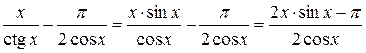 .
.
Внаслідок перетворень ми дістали невизначеність виду 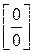 . Застосуємо правило Лопіталя
. Застосуємо правило Лопіталя
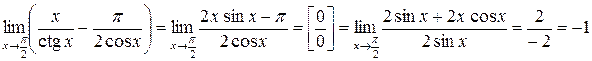 .
.
При розкритті невизначеностей типу 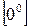 ,
, 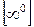 ,
, 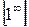 за допомогою правила Лопіталя попередньо необхідно виконати деякі перетворення.
за допомогою правила Лопіталя попередньо необхідно виконати деякі перетворення.
Нехай треба обчислити границю складеної степеневопоказникової функції:
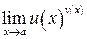 ,
,
де ми маємо невизначеність одного з вищезгаданих типів. Запишемо цю границю у вигляді
 ,
,
тут в показнику маємо вже невизначеність виду 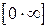 , яку можна звести до невизначеності типу
, яку можна звести до невизначеності типу 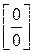 або
або 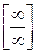 шляхом знесення в знаменник одного із співмножників, що стоять під знаком границі.
шляхом знесення в знаменник одного із співмножників, що стоять під знаком границі.
Приклад 3.32. Обчислити границю 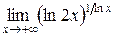 .
.
Розв’язання. Маємо невизначеність типу 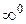 . Виконаємо тотожне перетворення функції:
. Виконаємо тотожне перетворення функції:
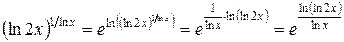 .
.
Знайдемо границю показника отриманої функції за правилом Лопіталя
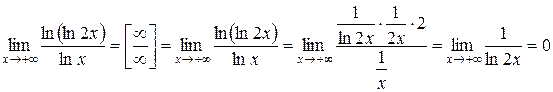 .
.
Отже, 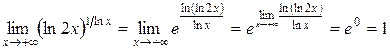 .
.
Приклад 3.33. Обчислити границю 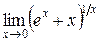 .
.
Розв’язання. Маємо невизначеність типу 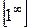 . Виконаємо тотожне перетворення функції, що стоїть під знаком границі:
. Виконаємо тотожне перетворення функції, що стоїть під знаком границі:
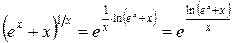 .
.
Обчислимо окремо границю, яка міститься в показнику, за правилом Лопіталя
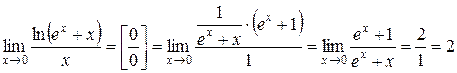 .
.
Отже,
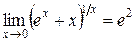 .
.
28. Необхідні та достатні умови екстремуму функції.
\ Екстремум (рос. экстремум, англ. extremum, нім. Extremum n) – найбільше та найменше значення функції на заданій множині.
29. Розкладення за формулою Маклорена деяких елементарних функцій.
Розкладання елементарних функцій в ряд Маклорена
інші роботи вид роботи: реферат; мова: українська
Рядом Маклорена функції f(x) називають степеневий ряд по степенях х, який можна дістати з ряду (38) при х0 = 0: (41) З п. 2.4 випливає таке правило розкладання функції в ряд: щоб функцію f(x) розкласти в ряд Маклорена потрібно: а) знайти похідні f´(х), f˝(х),...., fп(х),...; б) обчислити значення похідних в точці х = 0; в) записати ряд Маклорена (41) для даної функції і знайти інтервал його збіжності; г) визначити інтервал (–R; R), в якому залишковий член формули Маклорена Rп (х) → 0 при п → ∞. Якщо такий інтервал існує (він може відрізнятись від інтервалу збіжності ряду (41)), то в цьому інтервалі функція f (х) і сума ряду Маклорена збігаються: Розглянемо ряди Маклорена деяких елементарних функцій (вони часто використовуються і...
30. Розкладення за формулою Тейлора деяких елементарних функцій.
Ряд Те́йлора — разложение функции в бесконечную сумму степенных функций.
Для функції, яка диференційовна 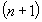 раз включно в околі точки
раз включно в околі точки 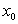 має місце формула Тейлор а:
має місце формула Тейлор а:
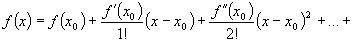
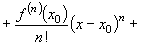
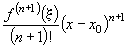 ,
, 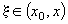 .
.
Останній доданок у формулі Тейлора
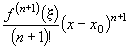
31. Поняття первісної функції та невизначеного інтеграла. Таблиця основних інтегралів.
Первісна функція. Означення.
Функція F(x) на заданому проміжку називається первісною для функції f(x), для всіх x з цього проміжку, якщо F'(x)=f(x).
Операція знаходження первісної для функції називається інтегруванням. Вона є оберненою до операції диференціювання.
Теорема.
Всяка неперервна на проміжку функція (x) має первісну на цьому проміжку.
Теорема (основна властивість первісної). Якщо на деякому проміжку функція F(x) є первісною для функції f(x), то на цьому проміжку первісною для f(x) буде також функція F(x)+C, де C довільна стала.
З цієї теореми випливає, що коли f(x) має на заданому проміжку первісну функцію F(x), то цих первісних безліч. Надаючи C довільних числових значень, кожного разу діставатимемо первісну функцію.
Для знаходження первісних користуються таблицею первісних. Вона отримується із таблиці похідних.
Невизначений інтеграл. Означення.
Множина всіх первісних функцій для функції f(x) називається невизначеним інтегралом і позначається  .
.
При цьому f(x) називається підінтегральною функцією, а f(x)dx - підінтегральним виразом.
Отже, якщо F(x), є первісною для f(x), то 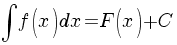 .
.
Властивості невизначеного інтегралу
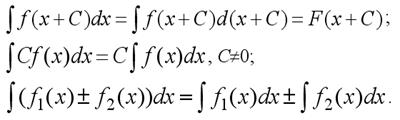
| Таблиця основних інтегралів |
1.. 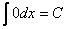
|
2. 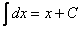 . .
|
3. 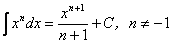 . .
|
4.  . .
|
5. 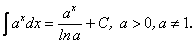
|
6. 
|
7. 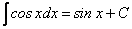 . .
|
8. 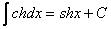
|
9. 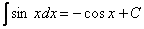 . .
|
10. 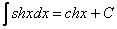 . .
|
11. 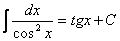 . .
|
12. 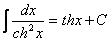 . .
|
13. 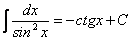 . .
|
14. 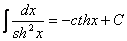 . .
|
15. 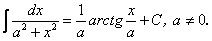
|
16. 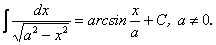
|
17. 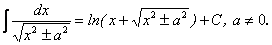
|
18. 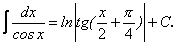
|
19. 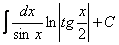 . .
|
20. 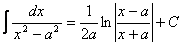 . .
|
21. 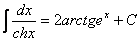 . .
|
22. 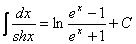 . .
|
23. 
|
32. Основні методи інтегрування: метод розкладення, метод підстановки (заміни змінної) та метод інтегрування частинами.
Інтегрування раціональних дробів. Метод розкладання.
Невизначений інтеграл від будь-якого раціонального дробу на всякому проміжку, на якому знаменник дробу не звертається в нуль, існує і виражається через елементарні функції, а саме він є алгебраїчною сумою суперпозиції раціональних дробів, арктангенсів і раціональних логарифмів.
Сам метод полягає в розкладанні раціонального дробу на суму найпростіших.
Усякий правильний раціональний дріб 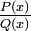 , знаменник якого розкладений на множники
, знаменник якого розкладений на множники
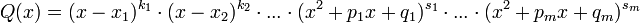 можна представити (і притім єдиним образом) у виді наступної суми найпростіших дробів:
можна представити (і притім єдиним образом) у виді наступної суми найпростіших дробів:
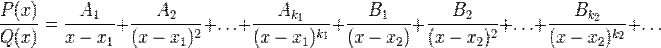
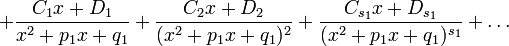
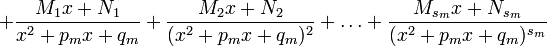
де 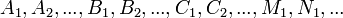 - деякі дійсні коефіцієнти. Звичайно невідомі коефіцієнти знаходяться за допомогою методу невизначених коефіцієнтів.
- деякі дійсні коефіцієнти. Звичайно невідомі коефіцієнти знаходяться за допомогою методу невизначених коефіцієнтів.
Метод підстановки (заміни змінної)
Цей метод містить два прийоми.
a) Якщо для знаходження заданого інтеграла ∫f(x)dx зробити підстановку x = φ(t), тоді має місце рівність
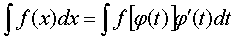
Після знаходження останнього інтеграла треба повернутись до початкової змінної інтегрування х. Для застосування цього прийому треба; щоб функція х - φ (t) мала обернену t = ψ(х).
Приклад. Знайти інтеграл
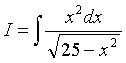
Розв'язування. Зробимо підстановку х = 5sint, тоді
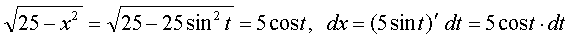
Отже, одержимо
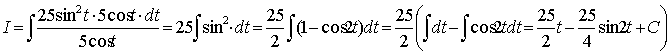
Із рівності х = 5sin t одержимо t = arcsin (х/5);
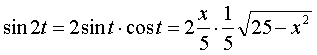
Отже, 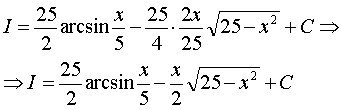
b) Якщо зробити заміну змінної, тобто t = φ (х) тоді має місце
рівність 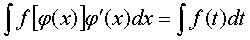
Після знаходження останнього інтеграли треба повернутись до змінної х, використовуючи рівність t = φ (х).
Приклад. Знайти 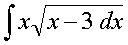
Розв’язування. Нехай  тоді
тоді 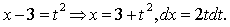
Тому 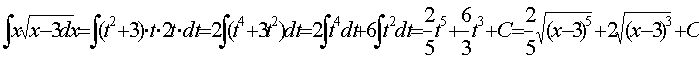
Метод інтегрування частинами
Цей метод застосовується тоді, коли під інтегралом є добуток функцій, причому хоча би одна з них є трансцендентною (не степеневою).
Формула інтегрування частинами:
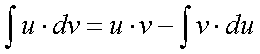
Ця формула дозволяє знаходження інтеграла 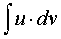 звести до знаходження інтеграла
звести до знаходження інтеграла 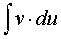 . При вдалому обранні u то dv інтеграл може бути табличним або простішим ніж заданий інтеграл
. При вдалому обранні u то dv інтеграл може бути табличним або простішим ніж заданий інтеграл 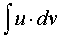
Приклад. Знайти 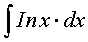
Розв'язування. Нехай u = Inx, dv = dx. Тоді 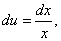 v = x
v = x
За формулою інтегрування частинами одержимо
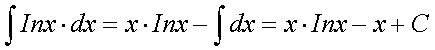
33. Поняття визначеного інтеграла. Обчислення визначеного інтеграла.
Означення.
Гранця інтегральної суми коли n→∞ називається визначеним інтегралом, і записується це так: 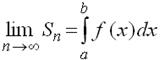 .
.
читається: "інтеграл від a до b f від xdx"
Число а називається нижньою межею інтегрування, b – верхньою межею інтегрування, відрізок [a; b] – проміжок інтегрування.
Властивості визначеного інтегралу
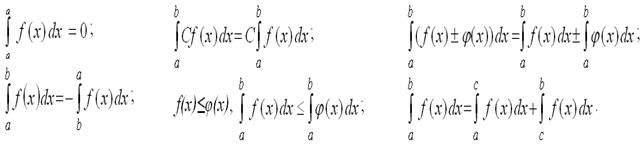
Формула Ньютона-Лейбніца
Визначений інтеграл тісно пов’язаний із первісною та невизначеним інтегралом формулою Ньютона- Лейбніца
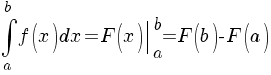 .
.
Інтеграл Рімана
Інтеграл Рімана - найпростіший із визначених інтегралів, є границею інтегральної суми. Для функції однієї змінної 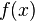 , визначеній на відрізку [a,b] та певного розбиття R цього відрізку на відрізки
, визначеній на відрізку [a,b] та певного розбиття R цього відрізку на відрізки 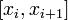 інтегральна сума визнається як
інтегральна сума визнається як
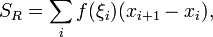
де 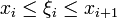 - будь-яка точка з відрізку.
- будь-яка точка з відрізку.
Якщо існує границя таких сум при прямуванні найбільшої довжини відріку 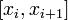 до нуля, то функція
до нуля, то функція 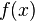 називається інтегрованою, а границя інтегральної суми називається інтегралом Рімана функції на відрізку
називається інтегрованою, а границя інтегральної суми називається інтегралом Рімана функції на відрізку 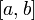 і позначається
і позначається
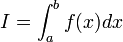 .
.
Інтеграл Рімана
Інтеграл Рімана - найпростіший із визначених інтегралів, є границею інтегральної суми. Для функції однієї змінної 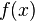 , визначеній на відрізку [a,b] та певного розбиття R цього відрізку на відрізки
, визначеній на відрізку [a,b] та певного розбиття R цього відрізку на відрізки 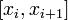 інтегральна сума визнається як
інтегральна сума визнається як
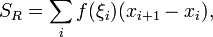
де 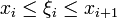 - будь-яка точка з відрізку.
- будь-яка точка з відрізку.
Якщо існує границя таких сум при прямуванні найбільшої довжини відріку 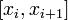 до нуля, то функція
до нуля, то функція 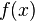 називається інтегрованою, а границя інтегральної суми називається інтегралом Рімана функції на відрізку
називається інтегрованою, а границя інтегральної суми називається інтегралом Рімана функції на відрізку 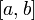 і позначається
і позначається
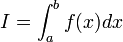 .
.
34. Заміна змінної та інтегрування частинами у визначеному інтегралі. Застосування визначеного інтеграла.
Замена переменной в определённом интеграле. Теорема. Пусть функция 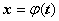
1. определена, непрерывно дифференцируема и монотонна на отрезке  ,
,
2. 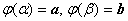 ,
,
3. функция  непрерывна на отрезке [ a, b ].
непрерывна на отрезке [ a, b ].
Тогда 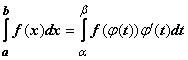 .
.
 Док-во. Пусть F (x) - первообразная для функции f (x), т.е.
Док-во. Пусть F (x) - первообразная для функции f (x), т.е. 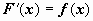 , тогда
, тогда 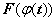 - первообразная для функции
- первообразная для функции 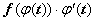 .
. 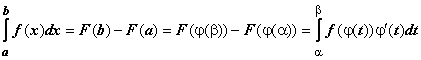 , что и требовалось доказать.
, что и требовалось доказать.
 При решении задач нельзя забывать о том, что при переходе к новой переменной надо обязательно вычислить новые пределы интеграла.
При решении задач нельзя забывать о том, что при переходе к новой переменной надо обязательно вычислить новые пределы интеграла.
 Пример:
Пример:
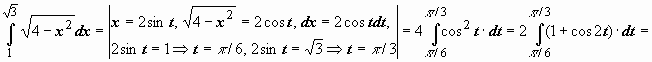
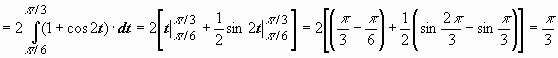 .
.
Формула интегрирования по частям для определённого интеграла. Если u (x), v (x) - непрерывно дифференцируемые функции, то 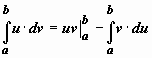 .
.
 Док-во. Интегрируем равенство
Док-во. Интегрируем равенство 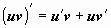 в пределах от a до b:
в пределах от a до b: 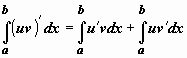 . Функция в левом интеграле имеет первообразную uv, по формуле Ньютона-Лейбница
. Функция в левом интеграле имеет первообразную uv, по формуле Ньютона-Лейбница  , следовательно,
, следовательно, 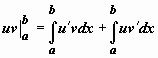 , откуда и следует доказываемое равенство.
, откуда и следует доказываемое равенство.
 Пример:
Пример: 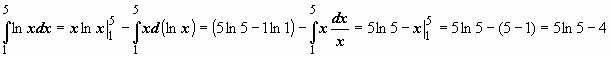
Застосування інтегралу
Інтегральне числення широко використовується при розв’язуванні різноманітних практичних задач. Розглянемо деякі з них.
Обчис Обчислення площі криволінійної трапеції
Обчислення об’ємів тіл
|
35. Невласні інтеграли першого роду.
Невласти́вий інтегра́л є розширенням поняття визначений інтеграл; він дозволяє в деяких випадках обраховувати «інтеграл на нескінченості» або «інтеграл від необмеженої функції». В математичному аналізі невластивим інтервалом називають границю послідовності визначених інтегралів, коли інтервал інтегрування збільшується до нескінченості, або коли інтервал наближається до особливої точки інтегрованої функції, де та йде у нескінченість.
Невласні інтеграли першого роду ("нескінчений інтервал")
Нехай функція 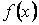 неперервна на проміжку
неперервна на проміжку 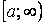 . Тоді вона буде неперервною на будь-якому скінченому відрізку
. Тоді вона буде неперервною на будь-якому скінченому відрізку  . Для функції
. Для функції 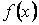 , неперервної на
, неперервної на  , існує визначений інтеграл
, існує визначений інтеграл 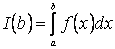 , який залежить від верхньої межі інтегрування. Цей інтеграл визначає деяку величину, наприклад площу криволінійної трапеції, обмеженої
, який залежить від верхньої межі інтегрування. Цей інтеграл визначає деяку величину, наприклад площу криволінійної трапеції, обмеженої
графіком функції 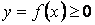 прямими
прямими 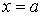 ,
, 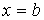 ,
, 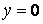 . Будемо необмежено збільшувати верхню межу інтегрування
. Будемо необмежено збільшувати верхню межу інтегрування 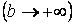 . При цьому можливі два випадки: або
. При цьому можливі два випадки: або 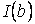 при
при 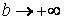 має скінчену границю, або не має.
має скінчену границю, або не має.
36. Невласні інтеграли другого роду.Невласні інтеграли
При введенні поняття визначеного інтегралу як границі інтегральної суми припускалось, що виконуються такі умови:
I. межі інтегрування 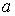 та
та  є скінченими;
є скінченими;
II. підінтегральна функція 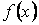 на
на 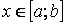 неперервна або має скінчене число точок розриву першого роду. В цьому випадку визначені інтеграли називаються власними. Якщо хоч одна з перечислених вище умов не виконується, то такі інтеграли називаються невласними. Невласні інтеграли є узагальненням визначених інтегралів на випадок нескінчених проміжків інтегрування та необмежених функцій.
неперервна або має скінчене число точок розриву першого роду. В цьому випадку визначені інтеграли називаються власними. Якщо хоч одна з перечислених вище умов не виконується, то такі інтеграли називаються невласними. Невласні інтеграли є узагальненням визначених інтегралів на випадок нескінчених проміжків інтегрування та необмежених функцій.
Невласні інтеграли другого роду
Нехай функція 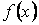 визначена і неперервна при
визначена і неперервна при  , а в точці
, а в точці  вона або невизначена, або має розрив другого роду. Тому говорити про інтеграл
вона або невизначена, або має розрив другого роду. Тому говорити про інтеграл 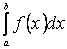 як про границю інтегральної суми неможливо, тому що функція
як про границю інтегральної суми неможливо, тому що функція 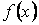 не є неперервною на відрізку
не є неперервною на відрізку 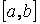 і, внаслідок цього, границя інтегральної суми, в класичному розумінні, не може існувати.
і, внаслідок цього, границя інтегральної суми, в класичному розумінні, не може існувати.
Означення 1. Якщо існує скінчена лівостороння границя 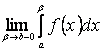 , то цю границю називають невласним інтегралом від розривної функції на відрізку
, то цю границю називають невласним інтегралом від розривної функції на відрізку 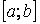 і вважають, що
і вважають, що
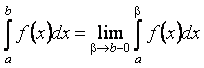 . (8.2.1)
. (8.2.1)
У цьому випадку інтеграл називають збіжним, а саму функцію 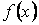 інтегрованою на відрізку
інтегрованою на відрізку 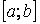 . Якщо границя рівна
. Якщо границя рівна 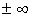 , або зовсім не існує, то інтеграл розбіжний.
, або зовсім не існує, то інтеграл розбіжний.
Аналогічно визначається невласний інтеграл другого роду, якщо функція неперервна при 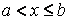 , а в точці
, а в точці 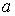 вона або невизначена, або має розрив другого роду:
вона або невизначена, або має розрив другого роду:
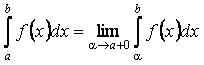 . (8.2.2)
. (8.2.2)
Якщо ж функція має розрив в деякій точці 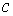 , яка лежить всередині відрізка
, яка лежить всередині відрізка 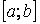 , то, згідно означення, вважають, що
, то, згідно означення, вважають, що
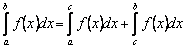 , (8.2.3)
, (8.2.3)
якщо два інтеграли, що лежать в правій частині існують.
37. Ознака збіжності невласних інтегралів.
Якщо функція 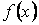 визначена і неперервна на відрізку
визначена і неперервна на відрізку 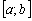 за виключенням скінченого числа точок
за виключенням скінченого числа точок 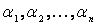 , які є внутрішніми точками відрізка і в цих точках має розриви другого роду, то інтеграл від функції
, які є внутрішніми точками відрізка і в цих точках має розриви другого роду, то інтеграл від функції 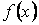 на відрізку
на відрізку 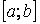 визначають так:
визначають так:
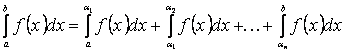 , (8.2.4)
, (8.2.4)
якщо кожен з невласних інтегралів в правій частині рівності (8.2.4) збігається, і сам інтеграл 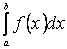 в цьому випадку називається збіжним.
в цьому випадку називається збіжним.
Якщо хоч би один з інтегралів в правій частині рівності розбігається, то і 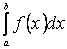 називається розбіжним.
називається розбіжним.
Для визначення збіжності невласних інтегралів від функцій, які мають розриви другого роду, використовують теореми аналогічні теоремам для визначення збіжності невласних інтегралів першого роду.
Теорема 3 Якщо функція 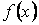 є знакозмінною на відрізку
є знакозмінною на відрізку 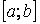 , має розрив другого роду в точці
, має розрив другого роду в точці  , і невласний інтеграл другого роду
, і невласний інтеграл другого роду 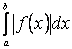 збігається, то збігається також невласний інтеграл
збігається, то збігається також невласний інтеграл 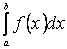 .
.
При виконанні умов теореми 3 невласний інтеграл другого роду 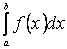 називається абсолютно збіжним.
називається абсолютно збіжним.
Date: 2015-09-18; view: 665; Нарушение авторских прав
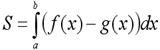
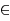 [a; b]. Тоді об’єм даного тіла можна знайти проінтегрувавши дану функцію у відповідних межах
[a; b]. Тоді об’єм даного тіла можна знайти проінтегрувавши дану функцію у відповідних межах