Суперпространство

Суперпространство -расширенное пространство в теории суперсимметрии, которое кроме обычных пространственно-временных координат включает также спинорные координаты.

Спинорные переменные 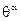антикоммутируют друг с другом и коммутируют с координатами пространства-времени :

,

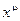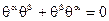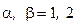
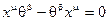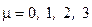, . (2.142)

Спинорные переменные могут рассматриваться как нечетные образующие грассмановой алгебры. Координаты 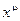служат четными образующими грассмановой алгебры (см. математическое приложение1). Антикоммутативность 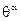необходима для обеспечения правильной связи спина со статистики. Важное следствие антикоммутативности грассмановых переменных - их нильпотентность:

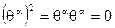для любого 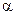(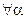). (2.143)

Концепция суперпространства играет ключевую роль в суперсимметрии: группа преобразований суперсимметрии реализуется как группа движений в суперпространстве. а соответствующие супермультиплеты компактно представляются суперполями -функциями заданными на суперпространстве.

Для простой суперсимметрии 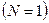известны вещественное суперпространство 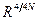и комплексное суперпространство :

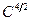. (2.144)

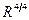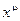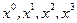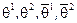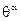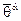
Суперпространство содержит, наряду с векторной координатой (4 четных координаты ), дополнительные (4 нечетных координаты ) спинорные координаты , 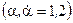. Спинорные координаты объединяются в вещественный майорановский спинор .

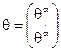Киральное суперпространство, содержащее в 2 раза меньше спинорных координат чем 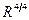, это

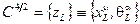. (2.145)

Оно является комплексным и его спинорные координаты образуют двухкомпонентный (левый 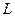) вейлевский спинор .

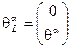В отсутствие гравитации вещественное суперпространство 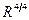есть гиперповерхность в комплексном суперпространстве 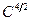, определяемая уравнениями

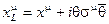
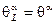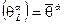, . (2.146)

здесь черта означает комплексное сопряжение, 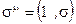, 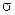-матрицы Паули.

Группой простой супергравитации является группа общих преобразований кирального суперпространства :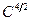

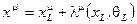
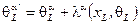(2.147)

ограниченных условием, что их супердетерминант (березиан) равен единицей:

.

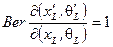это означает, что суперобъем 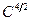сохраняется. Инфинитезимально (в случае бесконечно малого преобразования) это условие имеет вид

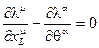
Простейшим неприводимым суперполем является киральное суперполе

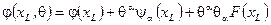(2.148)

описывающее скалярный супермультиплет вне массовой поверхности.

Этот супермультиплет включает в себя:

1. два вещественных поля- скалярное и псевдоскалярное

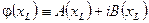, (спин=0),

2.спинор 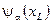(спин 1/2),

3. и два вещественных вспомогательных поля

.

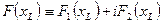Date: 2015-09-05; view: 401; Нарушение авторских прав