Супергравитация

Супергравитация- суперсимметризованная теория тяготения, т.е. теория тяготения Эйнштейна для системы материальных полей инвариантной относительно простой или расширенной суперсимметрии. Она представляет собой теорию с локализованной калибровочной суперсимметрией. В соответствии с числом N майорановских спинорных генераторов супергравитацию называют п р о с т о й (N =1) или расширенной (N >1). В этом смысле обычная теория гравитации является N =0 супергравитацией (без спинорных генераторов). Далее рассматривается только простая супергравитация.

Переносчик поля тяготения в супергравитации входит в один супермультиплет со своими суперпартнерами. В простой суперсимметрии гравитационный супермультиплет состоит из гравитона, описываемого тетрадой 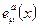(спиральность 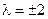) где , и одного гравитино, описываемого полем Рариты-Швингера (спиральность ), где 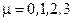-векторный индекс и спинорный индекс 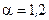4-мерного касательного пространства.

Действие для простой супергравитации имеет вид

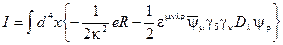(2.149)

где 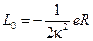- обычный лагранжиан для скалярного действия Эйнштейна-Гильберта. скалярная кривизна пространства. 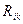-тензор Риччи связан с тензором кривизны пространста.

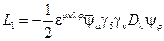- рарита-швингеровский лагранжиан для гравитино взаимодействующего с полем тяготения. Он возникает в результате замены производной 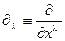на ковариантную производную 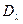включающую нужную лоренцеву связность,

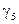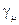, -матрицы Дирака, 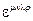-символ Леви-Чивита.

Инвариантность действия. Локальная суперсимметрия. Действие (2.149) инвариантно относительно группы общих координатных преобразований пространства и времени:

координаты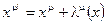

тетрада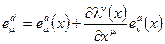

спин-векторное поле 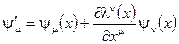(2.150)

здесь 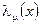-инфинизимальный векторный параметр, произвольная функция пространственно-временной точки х.

Действие (2.149) инвариантно также относительно преобразований локальной суперсимметрии со спинорными параметрами 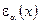. В инфинитезимальной форме (т.е.преобразований около единицы) они имеют вид:

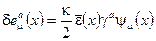
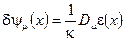(2.151)

В случае, когда параметры 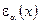зависят от х, преобразования (2.151) являются локальными преобразования суперсимметрии.

Суперпространство.Преобразования локальной суперсимметрии (2.151) и группа общекоординатных преобразований пространства-времени (2.150) объединяются в супергруппу общекоординатных преобразований суперпространства. Для простой суперсимметрии 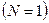известны вещественное суперпространство 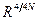и комплексное суперпространство :

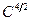. (2.152)

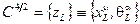(2.153)

Гравитационное аксиальное суперполе определяется следующими геометрическим образом. В комплексном суперпространстве 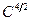вводится вещественная гиперповерхность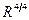

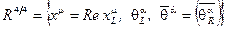(2.154)

Мнимая часть векторной координаты отождествляется с аксиальным гравитационным суперполем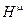

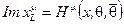(2.155)

Группа общих преобразований координат

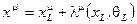
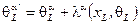(2.156)

индуцирует на нем калибровочные преобразования.

Минимизируя инвариантный суперобъем 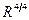, т.е варьируя действие (2.149) по 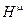, получаем на языке обычных компонентных полей уравнения Эйнштейна, уравнение Рариты-Швингера и уравнения вспомогательных полей, последние необходимы для замыкания алгебры локальных суперсимметрий и независимости их преобразований от конкретных моделей.

Нелинейные уравнения Эйнштейна (уравнения гравитационного поля) без космологической постоянной имеют вид

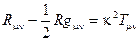(2.157)

где 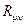-тензор Риччи, 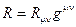, 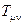-тензор энергии-импульса материи, ,

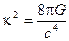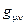- метрический тензор, входит в состав квадрата пространственно-временного интервала 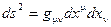, где 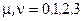, ( 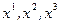-произвольные пространственные координаты, 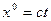-временная координата).

Ковариантизированное уравнение Рариты-Швингера для гравитино

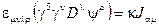(2.158)

где -сохраняющийся ток суперсимметрии.

Сравним это уравнение с лагранжианом Рариты-Швингера в действии

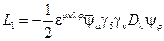. (2.159)

В заключение приведем высказывание математика Лейтеса Д. А.: «Мы живем в (4,4)-мерном супермногообразии, подстилающим многообразием которого является обычное 4-мерное пространство-время. Группой преобразования этого супермногообразия является супергруппа Ли, точки которой составляет группа Пуанкаре».

Date: 2015-09-05; view: 369; Нарушение авторских прав