
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Формула преобразования координат вектора линейного пространства при преобразовании его базиса
|
|
Пусть системы векторов e = {e 1,..., e n } и f = {f 1,..., f n } — два базиса n-мерного линейного пространства Ln.
Обозначим xe = (x1,x2,..., x n) и xf = (x'1,x'2,..., x' n) — координаты вектора x ∈ Ln соответственно в базисах e и f.
Справедливо следующее xe = C e→f ·x f:

Здесь C e→f — матрица перехода от базиса e к базису f, это матрица, столбцами которой являются координаты базисных векторов f1,..., f n в базисе e 1,..., en:
f1 = с11· e2 + с21 ·e1+... + с n 1 ·e n, f2 = с12· e1 + с22 ·e2+... + с n 2 ·e n, ..., f n = с1 n · e2 +... + с nn ·e n.
Формулу преобразования координат вектора при изменении базиса принято записывать в виде
xf = (C e→f)− 1 ·x e
Докажите, что если 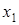 и
и 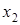 – собственные векторы оператора φ, относящиеся к одному и тому же собственному значению λ, то их линейная комбинация
– собственные векторы оператора φ, относящиеся к одному и тому же собственному значению λ, то их линейная комбинация 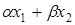 – собственный вектор оператора φ, относящийся к тому же собственному значению.
– собственный вектор оператора φ, относящийся к тому же собственному значению.
Доказательство:
Пусть х1 и х2 – собственные векторы, относящиеся к собственному значению λ, т.е. φ(х1) = λ* х1, φ(х2) = λ* х2
Покажем, что φ(α*х1 + β* х2) = λ(αх1 + βх2)
φ(α*х1 + β* х2) = α* φ(х1) + β* φ(х2) = αλ х1 + βλ х2 = λ(α х1 + β х2)
Доказать, что если векторы 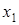 и
и 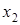 относятся к различным собственным значениям
относятся к различным собственным значениям 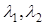 , то они линейно независимы.
, то они линейно независимы.
Доказательство:
x1 – c.в., относящийся к с.з. λ1 => φ(x1) = λ1 x1
x2 – с.в., относящийся к с.з. λ2 => φ(x2) = λ2 x2
λ1 ≠ λ2
Пусть векторы x1 и x2 – линейно зависимы => x1 =λ x2
φ(x1) = φ(αx2) = α φ(x2) = αλ2 x2 = λ2 (αx2) = λ2 x1 => x1 – c.в., относящийся к с.з. λ2, что противоречит условию.
Аналогично, φ(x2).
ð λ1 = λ2
ð x1 и x2 – линейно независимы.
Характеристический многочлен линейного оператора не зависит от выбора базиса
Доказательство.
Пусть А и A1 матрицы линейного оператора в базисах е1,е2…еn и f1,f2…fn. Преобразуем характеристический многочлен |A1-ƛE |, полученный в новом базисе f1,f2…fn если известна матрица перехода «Т» от старого базиса е1,е2…еn к базису f1,f2…fn.
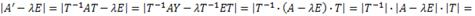
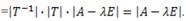
Общее уравнение прямой на плоскости
ЗАДАЧА 11.1. Записать уравнение прямой, проходящей через точку 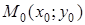 , перпендикулярно вектору
, перпендикулярно вектору 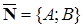 .
.
Пусть точка 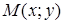 – произвольная точка прямой (такую точку мы будем в дальнейшем называть текущей точкой прямой). Обозначим через
– произвольная точка прямой (такую точку мы будем в дальнейшем называть текущей точкой прямой). Обозначим через 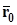 и
и 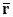 – радиус-векторы точек
– радиус-векторы точек 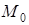 и
и 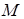 соответственно. Рассмотрим векторы
соответственно. Рассмотрим векторы 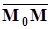
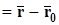 и
и  . По условию задачи они перпендикулярны. Следовательно,
. По условию задачи они перпендикулярны. Следовательно, 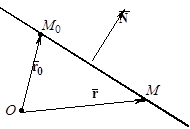
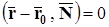 ,(23)
,(23)
или, в координатной форме, 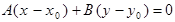 .(24)
.(24)
Уравнению (24) удовлетворяют координаты любой точки прямой и не удовлетворяют координаты других точек плоскости. Следовательно, это и есть искомое уравнение. Уравнения (23) и (24) называют уравнениями прямой, проходящей через точку 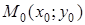 перпендикулярно вектору
перпендикулярно вектору 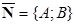 (в векторной и координатной форме соответственно).
(в векторной и координатной форме соответственно).
Раскроем скобки в уравнении (24) и приведем подобные слагаемые: 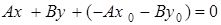 .
.
Обозначим число 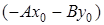 через
через 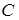 и получим общее уравнение прямой на плоскости:
и получим общее уравнение прямой на плоскости:
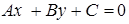 . (25)
. (25)
Таким образом, прямая в общем случае она задается уравнением (25), где 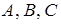 – числа. Причем
– числа. Причем 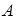 и
и 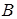 не обращаются в ноль одновременно, так как с геометрической точки зрения это коэффициенты вектора, перпендикулярного прямой. Вектор, перпендикулярный прямой, называют нормальнымвектором этой прямой.
не обращаются в ноль одновременно, так как с геометрической точки зрения это коэффициенты вектора, перпендикулярного прямой. Вектор, перпендикулярный прямой, называют нормальнымвектором этой прямой.
Параметрические уравнения прямой
Получим параметрические уравнение прямой на плоскости, решив следующую задачу.
ЗАДАЧА 11.2. Записать уравнение прямой, проходящей через точку 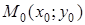 , пар-о вектору
, пар-о вектору 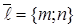 .
.
Вектор, параллельный прямой, называют направляющим вектором этой прямой.
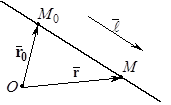 Пусть точка
Пусть точка 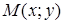 – текущая точка прямой. Обозначим через
– текущая точка прямой. Обозначим через 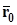 и
и 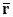 – радиус-векторы точек
– радиус-векторы точек 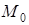 и
и 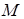 соответственно. Рассмотрим векторы
соответственно. Рассмотрим векторы 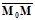
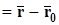 и
и 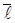 . По условию задачи они параллельны. Следовательно, существует такое число
. По условию задачи они параллельны. Следовательно, существует такое число  , что
, что 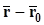
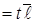 , ⇒
, ⇒ 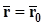
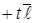 , (27)
, (27)
или, в координатной форме,
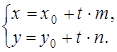 (28)
(28)
Очевидно, что системе (28) будут удовлетворять координаты любой точки прямой при некотором значении  (
( называют параметром) и не будут удовлетворять координаты других точек плоскости.
называют параметром) и не будут удовлетворять координаты других точек плоскости.
Уравнение (27) и систему уравнений (28) называют параметрическимиуравнениями прямой (в векторной и координатной форме соответственно).
Каноническое уравнение прямой на плоскости
Если в задаче 11.2 вектор 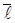 не параллелен ни одной из координатных осей (т.е. если
не параллелен ни одной из координатных осей (т.е. если 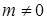 и
и 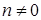 ), то из уравнений системы (28) можно выразить параметр
), то из уравнений системы (28) можно выразить параметр  :
: 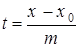 и
и 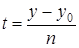 ,
,
и заменить систему (28) одним уравнением вида: 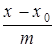
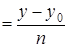 , (29)
, (29)
где 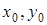 – координаты некоторой точки на прямой,
– координаты некоторой точки на прямой, 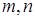 – координаты направляющего вектора прямой.
– координаты направляющего вектора прямой.
Уравнение (29) называют каноническим уравнением прямой на плоскости.
Уравнение прямой, проходящей через две точки
Это уравнение является частным случаем канонического уравнения прямой.
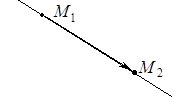 Действительно, пусть прямая проходит через две точки
Действительно, пусть прямая проходит через две точки  и
и 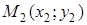 . Тогда вектор
. Тогда вектор 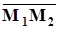
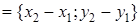 является ее направляющим вектором и каноническое уравнение этой прямой будет иметь вид
является ее направляющим вектором и каноническое уравнение этой прямой будет иметь вид
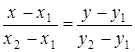 . (30)
. (30)
Уравнение (30) называют уравнением прямой, проходящей через две точки  и
и 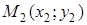 .
.
Общее уравнение плоскости
Получим общее уравнение плоскости, решив следующую задачу.
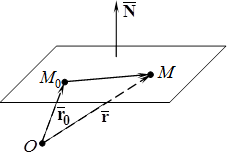 ЗАДАЧА 12.1. Записать уравнение плоскости, проходящей через точку
ЗАДАЧА 12.1. Записать уравнение плоскости, проходящей через точку 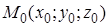 , перпендикулярно вектору
, перпендикулярно вектору 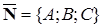 .
.
Пусть точка 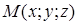 – текущая точка плоскости. Обозначим через
– текущая точка плоскости. Обозначим через 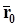 и
и 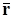 – радиус-векторы точек
– радиус-векторы точек 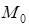 и
и 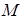 соответственно. Рассмотрим векторы
соответственно. Рассмотрим векторы 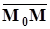
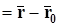 и
и 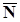 . По условию задачи они перпендикулярны. Следовательно,
. По условию задачи они перпендикулярны. Следовательно, 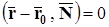 ,(36)
,(36)
или, в ко-й форме, 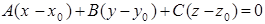 . (37)
. (37)
Уравнению (37) удовлетворяют координаты любой точки рассматриваемой плоскости и не удовлетворяют координаты других точек пространства. Следовательно, это и есть искомое уравнение. Уравнения (36) и (37) называют уравнениями плоскости, проходящей через точку 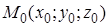 перпендикулярно вектору
перпендикулярно вектору 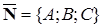 (в векторной и координатной форме соответственно).
(в векторной и координатной форме соответственно).
Раскроем скобки в уравнении (37) и приведем подобные слагаемые: 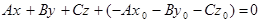
Об-м число 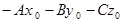 через
через 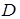 и получим общее уравнение пл-ти:
и получим общее уравнение пл-ти: 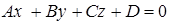 (38)
(38)
Таким образом, плоскость является поверхностью первого порядка. В общем случае она задается уравнением (38), где 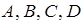 – числа. Причем
– числа. Причем 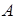 ,
, 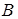 и
и 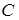 не обращаются в ноль одновременно, так как с геометрической точки зрения это коэффициенты вектора, перпендикулярного плоскости.
не обращаются в ноль одновременно, так как с геометрической точки зрения это коэффициенты вектора, перпендикулярного плоскости.
Другие формы записи уравнения плоскости
Рассмотрим в каком еще виде можно записать уравнение плоскости.
1) Уравнение плоскости, проходящей через точку параллельно двум неколлинеарным векторам
Решим следующую задачу.
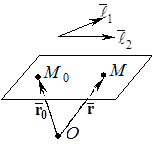 ЗАДАЧА 12.2. Записать уравнение плоскости, проходящей через точку
ЗАДАЧА 12.2. Записать уравнение плоскости, проходящей через точку 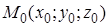 , параллельно неколлинеарным векторам
, параллельно неколлинеарным векторам 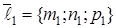 и
и 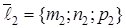 .
.
Пусть точка 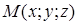 – текущая точка плоскости. Обозначим через
– текущая точка плоскости. Обозначим через 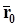 и
и 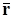 – радиус-векторы точек
– радиус-векторы точек 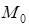 и
и 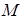 соответственно. Рассмотрим векторы
соответственно. Рассмотрим векторы
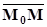
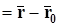 ,
, 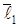 и
и 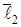 . По условию задачи они компланарны. Следовательно,
. По условию задачи они компланарны. Следовательно,
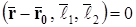 ,(40) или, в ко-ой форме,
,(40) или, в ко-ой форме, 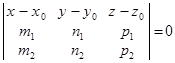 (41)
(41)
Уравнения (40) и (41) называют уравнениями плоскости, проходящей через точку параллельно двум неколлинеарным векторам (в векторной и координатной форме соответственно).
Уравнение плоскости, проходящей через три точки, не лежащие на одной прямой
Это уравнение является частным случаем уравнения (41).
Действительно, пусть плоскость проходит через три точки 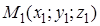 ,
, 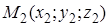 и
и 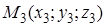 , не лежащие на одной прямой. Тогда векторы
, не лежащие на одной прямой. Тогда векторы
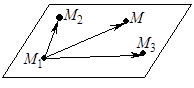

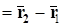
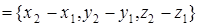
и 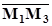
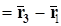
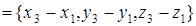
неколлинеарные и параллельны плоскости. Следовательно, уравнение этой плоскости будет иметь вид 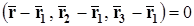 , (42)
, (42)
или в координатной форме
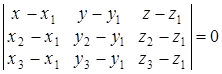 . (43)
. (43)
Уравнения (42) и (43) называют уравнениями плоскости, проходящей через три точки 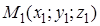 ,
, 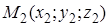 и
и 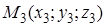 (в векторной и координатной форме соответственно).
(в векторной и координатной форме соответственно).
Исследование
Проведем исследование общего уравнения плоскости. Т.е. выясним, что можно сказать о плоскости по виду ее общего уравнения. Если в уравнении (38) все коэффициенты 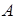 ,
,  ,
,  и
и 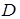 отличны от нуля, то уравнение называют полным; если хотя бы один из коэффициентов равен нулю – уравнение называют неполным.
отличны от нуля, то уравнение называют полным; если хотя бы один из коэффициентов равен нулю – уравнение называют неполным.
 1) Пусть уравнение (38) – полное. Тогда его можно записать в виде
1) Пусть уравнение (38) – полное. Тогда его можно записать в виде
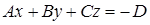 , ⇒
, ⇒ 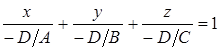 .
.
Обозначим 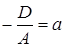 ,
, 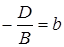 и
и 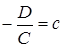 . Тогда уравнение плоскости примет вид
. Тогда уравнение плоскости примет вид 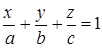 . (39)
. (39)
Уравнение (39) называют уравнением плоскости в отрезках. Легко проверить, что плоскость, имеющая уравнение (39), проходит через точки 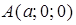 ,
, 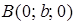 и
и 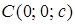 . Следовательно, с геометрической точки зрения
. Следовательно, с геометрической точки зрения 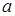 ,
, 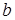 и
и 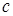 – отрезки, отсекаемые плоскостью на координатных осях
– отрезки, отсекаемые плоскостью на координатных осях 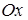 ,
, 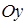 и
и 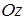 соответственно.
соответственно.
2) Пусть в уравнении (38) коэффициенты 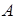 ,
, 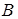 и
и 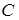 – ненулевые, а
– ненулевые, а 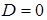 , т.е. уравнение плоскости имеет вид
, т.е. уравнение плоскости имеет вид
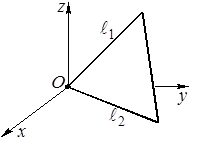
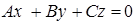 .
.
Легко проверить, что такая плоскость проходит через начало координат 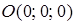 .
.
Замечание. Чтобы построить плоскость 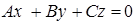 , обычно находят прямые, по которым она пересекается с двумя координатными плоскостями. Например,
, обычно находят прямые, по которым она пересекается с двумя координатными плоскостями. Например, 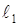 – пересечение с плоскостью
– пересечение с плоскостью 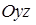 (ее уравнение
(ее уравнение 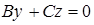 ) и
) и 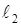 – пересечение с плоскостью
– пересечение с плоскостью 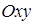 (ее уравнение
(ее уравнение 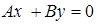 ).
).
3) Пусть в уравнении (38) один из коэффициентов 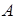 ,
, 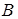 или
или 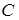 – нулевой, а
– нулевой, а 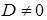 , т.е. уравнение плоскости имеет вид
, т.е. уравнение плоскости имеет вид 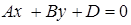 или
или  или
или 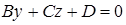 .
.
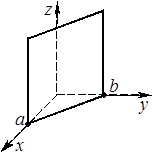 Если плоскость имеет уравнение
Если плоскость имеет уравнение 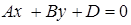 , то его можно записать в виде
, то его можно записать в виде 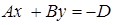 ,
,
⇒ 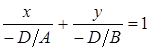 , ⇒
, ⇒ 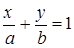 ,
,
где 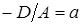 ,
, 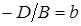 . Но последнему уравнению удовлетворяют координаты точек
. Но последнему уравнению удовлетворяют координаты точек 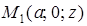 и
и 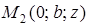 (при любом
(при любом  ). Следовательно, плоскость
). Следовательно, плоскость 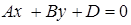 параллельна оси
параллельна оси 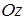 и отсекает на осях
и отсекает на осях 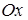 и
и 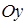 отрезки
отрезки 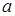 и
и 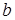 соответственно.
соответственно.
Аналогичным образом получаем, что плоскость  параллельна оси
параллельна оси 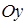 и отсекает на осях
и отсекает на осях 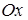 и
и 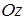 отрезки
отрезки 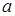
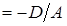 и
и 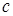
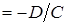 соответственно, а плоскость
соответственно, а плоскость 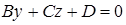 – параллельна оси
– параллельна оси 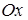 и отсекает на осях
и отсекает на осях 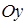 и
и 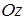 отрезки
отрезки 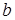
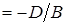 и
и 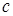
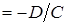 .
.
 |
Таким образом, плоскость, в уравнении которой отсутствует одна из координат, параллельна оси отсутствующей координаты.
4) Пусть в уравнении (38) два из трех коэффициентов 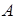 ,
, 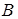 или
или 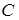 – нулевые, а
– нулевые, а 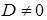 , т.е. уравнение плоскости имеет вид
, т.е. уравнение плоскости имеет вид 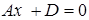 или
или 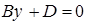 или
или 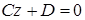 .
.
Если пл-ть имеет ур-ие 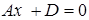 , то его можно записать в виде
, то его можно записать в виде 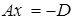 , ⇒
, ⇒ 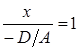 , ⇒
, ⇒ 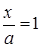 ,
,
где 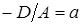 . Но последнему уравнению удовлетворяют координаты точек
. Но последнему уравнению удовлетворяют координаты точек 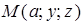 (при любых
(при любых 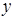 и
и 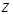 ). Следовательно, плоскость
). Следовательно, плоскость 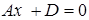 параллельна координатной плоскости
параллельна координатной плоскости 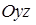 и отсекает на оси
и отсекает на оси 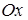 отрезок
отрезок 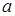
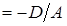 .
.
 |
Аналогичным образом получаем, что плоскость
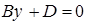 параллельна координатной плоскости
параллельна координатной плоскости 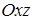 и отсекает на оси
и отсекает на оси 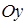 отрезок
отрезок 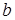
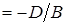 , а плоскость
, а плоскость 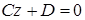 – параллельна плоскости
– параллельна плоскости 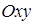 и отсекает на оси
и отсекает на оси 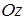 отрезок
отрезок 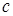
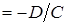 .
.
Таким образом, плоскость, в уравнении которой отсутствуют две координаты, параллельна координатной плоскости, проходящей через оси отсутствующих координат.
5) Пусть в уравнении (38) 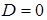 и один из коэффициентов
и один из коэффициентов 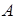 ,
, 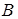 или
или 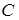 тоже нулевой, т.е. уравнение плоскости имеет вид
тоже нулевой, т.е. уравнение плоскости имеет вид 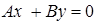 или
или 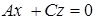 или
или 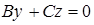 .
.
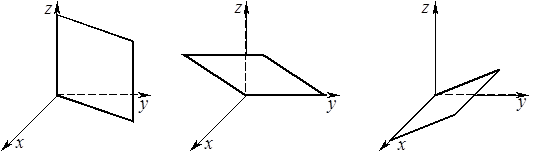
Уравнению 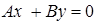 удовлетворяют координаты точек
удовлетворяют координаты точек 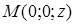 (при любом
(при любом 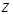 ). Следовательно, эта плоскость проходит через ось
). Следовательно, эта плоскость проходит через ось 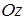 .
.
Ан-но получаем, что пл-ть 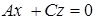 прох-т через ось
прох-т через ось 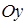 , а пл-ть
, а пл-ть 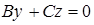 – прох-т через ось
– прох-т через ось 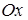 .
. 
5) Пусть в уравнении (38) три коэффициента равны нулю, т.е. уравнение плоскости имеет вид
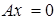 или
или  или
или 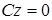 .
.
Эти уравнения можно записать соответственно в виде 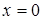 ,
, 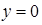 ,
,  .
.
Но это уравнения координатных плоскостей 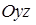 ,
, 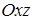 ,
, 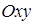 .
.
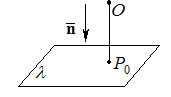 Замечание. Пусть плоскость
Замечание. Пусть плоскость 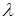 не проходит через начало координат,
не проходит через начало координат, 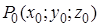 – основание перпендикуляра, опущенного на
– основание перпендикуляра, опущенного на 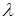 из начала координат,
из начала координат, 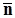
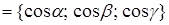 – орт вектора
– орт вектора 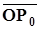 . Так как
. Так как 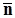 является нормальным вектором плоскости
является нормальным вектором плоскости 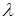 , то ее общее уравнение можно записать в виде
, то ее общее уравнение можно записать в виде 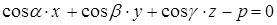 ,
,
где 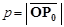 – расстояние от начала координат до плоскости
– расстояние от начала координат до плоскости 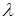 (доказать самим). Этот частный случай общего уравнения плоскости называется нормальным уравнением плоскости.
(доказать самим). Этот частный случай общего уравнения плоскости называется нормальным уравнением плоскости.
Для плоскости, проходящей через начало координат, тоже можно записать нормальное уравнение. В этом случае оно будет иметь вид 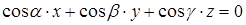 ,
,
где 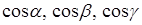 – направляющие косинусы нормали к плоскости.
– направляющие косинусы нормали к плоскости.
Уравнения прямой в пространстве
В аналитической геометрии любая пространственная линия рассматривается как пересечение двух поверхностей. Прямую в пространстве можно задавать как пересечение двух плоскостей. Действительно, пусть  и
и 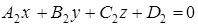 – уравнения непараллельных плоскостей. Тогда эти плоскости пересекаются по некоторой прямой
– уравнения непараллельных плоскостей. Тогда эти плоскости пересекаются по некоторой прямой 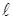 . Координаты любой точки прямой
. Координаты любой точки прямой 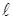 удовлетворяют одновременно обоим уравнениям, т.е. являются решениями системы
удовлетворяют одновременно обоим уравнениям, т.е. являются решениями системы
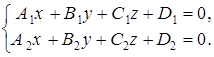 (46)
(46)
Систему (46) называют общими уравнениями прямой в пространстве. Так как через любую прямую в пространстве проходит множество плоскостей, то любую прямую можно задать ее общими уравнениями и не единственным образом.
При решении задач удобнее использовать другие, более наглядные формы записи уравнений прямой – параметрические или канонические уравнения.
Получим параметрические и канонические уравнение прямой в пространстве, решив следующую задачу.
ЗАДАЧА 13.1. Записать уравнение прямой в пространстве, проходящей через точку 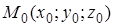 , параллельно вектору
, параллельно вектору 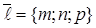 .
.
Также, как и для прямой на плоскости, вектор, параллельный прямой в пространстве, называют направляющим вектором этой прямой.
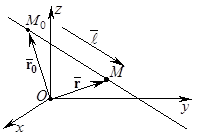 Пусть точка
Пусть точка 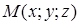 – текущая точка прямой. Обозначим через
– текущая точка прямой. Обозначим через 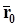 и
и 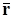 – радиус-векторы точек
– радиус-векторы точек 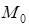 и
и 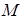 соответственно. Рассмотрим векторы
соответственно. Рассмотрим векторы 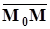
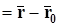 и
и 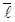 . По условию задачи они параллельны. Следовательно, существует такое число
. По условию задачи они параллельны. Следовательно, существует такое число 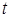 (
(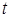 называют параметром), что
называют параметром), что
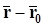
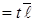 , ⇒
, ⇒ 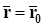
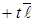 , (47) или, в координатной форме,
, (47) или, в координатной форме,
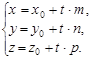 (48)
(48)
Уравнение (47) и систему уравнений (48) называют параметрическимиуравнениями прямой в пространстве (в векторной и координатной форме соответственно).
Если в задаче 13.1 вектор 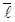 не параллелен ни одной из координатных плоскостей (т.е. если
не параллелен ни одной из координатных плоскостей (т.е. если 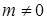 ,
, 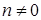 и
и 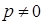 ), то из ур-й системы (48) можно выразить пар-тр
), то из ур-й системы (48) можно выразить пар-тр 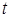 :
: 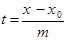 ,
, 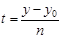 ,
, 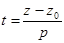
и заменить систему (48) одним уравнением вида: 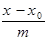
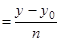
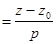 , (49)
, (49)
где  – координаты некоторой точки на прямой,
– координаты некоторой точки на прямой, 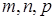 – координаты направляющего вектора прямой.
– координаты направляющего вектора прямой.
Уравнения (49) называют каноническими уравнениями прямой в пространстве.
Частным случаем канонических уравнений являются уравнения прямой, проходящей через две точки.
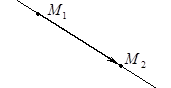 Действительно, пусть прямая проходит через две точки
Действительно, пусть прямая проходит через две точки 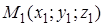 и
и 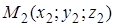 . Тогда вектор
. Тогда вектор 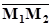

является ее направляющим вектором и канонические уравнения этой прямой будут иметь вид
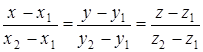 . (50)
. (50)
Уравнения (50) называют уравнениями прямой, проходящей через две точки 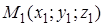 и
и 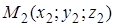 .
.
Каноническое уравнение эллипса (вывод)
ОПРЕДЕЛЕНИЕ. Эллипсом называется геометрическое место точек плоскости, сумма расстояний от которых до двух фиксированных точек плоскости 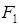 и
и 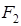 есть величина постоянная и равная
есть величина постоянная и равная 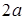 (
(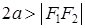 ). Точки
). Точки 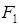 и
и 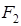 называют фокусами эллипса.
называют фокусами эллипса.
Получим уравнение эллипса. Выберем декартову прямоугольную систему координат так, чтобы фокусы 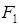 и
и 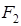 лежали на оси
лежали на оси 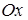 на одинаковом расстоянии от начала координат. В такой системе координат точки
на одинаковом расстоянии от начала координат. В такой системе координат точки 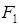 и
и 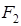 будут иметь координаты:
будут иметь координаты: 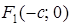 и
и 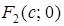 ,
,
где 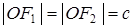 . Пусть
. Пусть 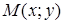 – текущая точка эллипса. По определению эллипса
– текущая точка эллипса. По определению эллипса
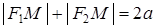 , ⇒
, ⇒ 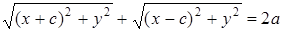 .
.
Избавимся от квадратных корней: 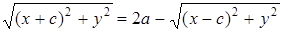 ,
,
⇒ 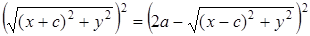 ,
,
⇒ 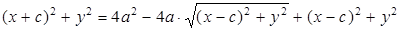 .
.
Приведя подобные слагаемые, получим: 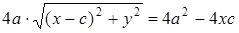 .
.
Снова возведем обе части в квадрат и приведем подобные слагаемые:
 , ⇒
, ⇒ 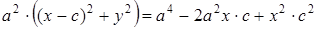 ,
,
⇒ 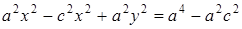 , ⇒
, ⇒ 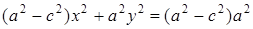 .
.
Так как по определению  , то
, то 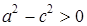 . Следовательно,
. Следовательно,  , для некоторого числа
, для некоторого числа 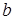 , и последнее равенство примет вид:
, и последнее равенство примет вид: 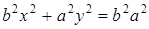 .
.
Разделим обе части этого равенства на 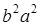 и окончательно получим:
и окончательно получим: 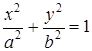 . (58)
. (58)
Уравнение (58) называется каноническим уравнением эллипса. Система координат, в которой эллипс имеет такое уравнение, называется его канонической системой координат.
Каноническое уравнение гиперболы в декартовой системе координат (вывод)
ОПРЕДЕЛЕНИЕ. Гиперболой называется геометрическое место точек плоскости, модуль разности расстояний от которых до двух фиксированных точек плоскости 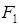 и
и 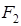 есть величина постоянная и равная
есть величина постоянная и равная 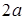 (
(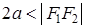 ). Точки
). Точки 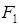 и
и 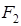 называют фокусами гиперболы.
называют фокусами гиперболы.
Получим уравнение гиперболы. Выберем декартову прямоугольную систему координат так, чтобы фокусы 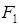 и
и 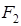 лежали на оси
лежали на оси 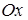 на одинаковом расстоянии от начала координат. В такой системе координат точки
на одинаковом расстоянии от начала координат. В такой системе координат точки 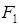 и
и 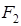 будут иметь координаты:
будут иметь координаты: 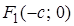 и
и 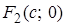 ,
,
где 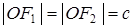 . Пусть
. Пусть 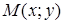 – текущая точка гиперболы. По определению гиперболы
– текущая точка гиперболы. По определению гиперболы
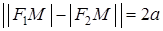 , ⇒
, ⇒ 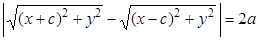 ,
,
⇒ 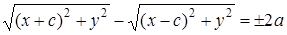 , Избавимся от квадратных корней:
, Избавимся от квадратных корней:
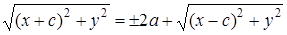 ⇒
⇒ 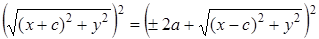 ,
,
⇒ 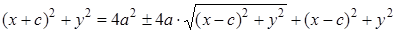 .
.
Приведя подобные слагаемые, получим: 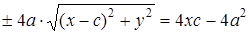 .
.
Снова возведем обе части в квадрат и приведем подобные слагаемые:
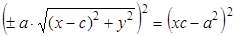 ⇒
⇒ 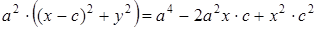 ,
,
⇒ 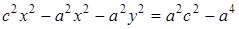 ⇒
⇒ 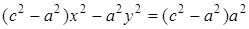 .
.
Так как по определению 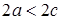 , то
, то 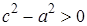 . Следовательно,
. Следовательно, 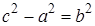 , для некоторого числа
, для некоторого числа 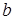 , и последнее равенство примет вид:
, и последнее равенство примет вид: 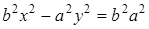 .
.
Разделим обе части этого равенства на 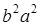 и окончательно получим:
и окончательно получим:  .(59)
.(59)
Уравнение (59) называется каноническим уравнением гиперболы. Система координат, в которой гипербола имеет такое уравнение, называется ееканонической системой координат.
Каноническое уравнение параболы в декартовой системе координат (с выводом)
Пусть 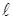 – некоторая прямая на плоскости,
– некоторая прямая на плоскости, 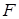 – некоторая точка плоскости, не лежащая на прямой
– некоторая точка плоскости, не лежащая на прямой 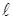 .
.
ОПРЕДЕЛЕНИЕ. Параболой называется геометрическое место точек плоскости, расстояние от которых до фиксированной прямой 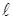 и до фиксированной точки
и до фиксированной точки 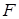 (не лежащей на прямой
(не лежащей на прямой 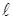 ) одинаково.
) одинаково.
Точку 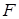 называют фокусом параболы, прямую
называют фокусом параболы, прямую 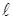 – директрисой.
– директрисой.
Получим уравнение параболы. Пусть 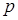 – расстояние от
– расстояние от 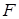 до
до 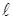 . Выберем декартову прямоугольную систему координат так, чтобы директриса параболы
. Выберем декартову прямоугольную систему координат так, чтобы директриса параболы 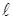 была перпендикулярна оси
была перпендикулярна оси 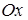 , фокус
, фокус 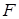 лежал на положительной части
лежал на положительной части 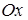 и расстояние от начала координат до фокуса и до директрисы было одинаковым. В такой системе координат
и расстояние от начала координат до фокуса и до директрисы было одинаковым. В такой системе координат
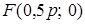 и
и 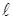 :
: 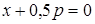 . Пусть
. Пусть 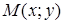 – текущая точка параболы. По определению пара.
– текущая точка параболы. По определению пара.
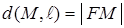 , т.е.
, т.е. 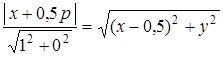 , ⇒
, ⇒ 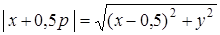 .
.
Избавимся от квадратного корня: 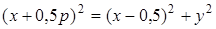 ⇒
⇒ 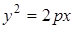 (61)
(61)
Уравнение (61) называется каноническим уравнением параболы. Система координат, в которой парабола имеет такое уравнение, называется ее канонической системой координат.
Date: 2015-09-05; view: 1775; Нарушение авторских прав