
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Свойства скалярного произведения векторов
|
|
1. Скалярное произведение векторов коммутативно, т.е. ( ,
,  ) = (
) = ( ,
, 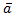 ).
).
( ,
,  ) = |
) = |  |∙ |
|∙ |  |∙ cos(
|∙ cos(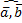 ), а (
), а ( ,
, 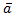 ) = |
) = |  |∙|
|∙|  |∙ cos(
|∙ cos(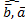 ). И так как
). И так как
|  |∙ |
|∙ |  |= |
|= |  |∙|
|∙|  |, как произведение чисел и cos(
|, как произведение чисел и cos(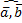 ) = cos(
) = cos(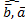 ), то
), то
( ,
,  ) = (
) = ( ,
, 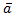 ).
).
2. Скалярное произведение ненулевых векторов  и
и  равно произведению длины вектора
равно произведению длины вектора 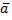 на проекцию вектора
на проекцию вектора  на вектор
на вектор  (длины вектора
(длины вектора  на проекцию
на проекцию  на
на  ). Так как
). Так как
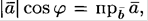
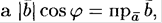 то получаем:
то получаем: 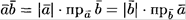 .
.
3. Числовой множитель любого из 2-х векторов можно вынести за знак скалярного произведения: (λ  ,
,  ) = (
) = ( , λ
, λ  ) = λ(
) = λ( ,
,  ).
).
4. 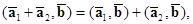 Если один из векторов записан в виде суммы, то их скалярное произведение тоже можно записать в виде суммы.
Если один из векторов записан в виде суммы, то их скалярное произведение тоже можно записать в виде суммы.
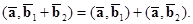 |
5. Скалярное произведение вектора на себя (скалярный квадрат вектора) равно квадрату его длины. Т.е. (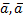 ) = |
) = |  |2.
|2.
(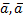 ) = |
) = |  |∙|
|∙|  | cos0 = |
| cos0 = |  |∙|
|∙|  | = |
| = |  |2.
|2.
|  | =
| = 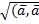 ).
).
6. Физический смысл скалярного произведения.
Если под действием постоянной силы 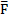 точка перемещается по прямой из т. М1 в М2, то работа силы
точка перемещается по прямой из т. М1 в М2, то работа силы 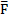 будет равна А = (
будет равна А = (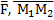 ).
).
Скалярное произведение векторов в декартовой системе координат (с выводом формулы).
Если в декартовом прямоугольном базисе векторы  и
и  имеют координаты:
имеют координаты:
 = {
= { 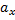 ;
; 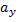 ;
; 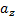 },
},  = {
= { 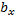 ;
; 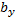 ;
; 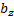 }, то (
}, то ( ,
,  ) =
) = 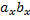 +
+ 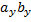 +
+ 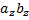
Доказательство
Пусть  =
= 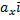 +
+  +
+ 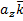 ;
;  =
= 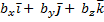 ;
;
Найдем ( ,
,  ) = (
) = (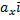 +
+ 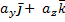 ,
, 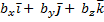 ) = (
) = (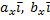 ) + (
) + (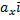 ,
, 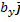 ) +
) +
+ (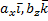 ) + (
) + (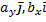 ) + (
) + (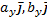 ) + (
) + (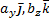 ) + (
) + (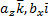 ) + (
) + (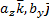 )+(
)+(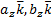 ) =
) = 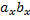 (
(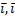 ) +
) + 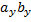 (
(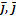 ) +
) + 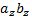 (
( ) =
) = 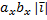 2 +
2 + 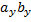 |
| 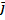 |2 +
|2 + 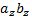 |
| 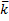 |2 =
|2 = 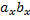 +
+ 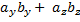 .
.
Критерий ортогональности (перпендикулярности) векторов (доказать).
Ненулевые векторы 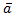 и
и  перпендикулярны тогда и только тогда, когда их скалярное произведение равно нулю.
перпендикулярны тогда и только тогда, когда их скалярное произведение равно нулю. 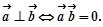
Доказательство:
Если векторы перпендикулярны, значит угол м/у ними равен 90. Тогда скалярное произведение запишется: (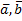 ) = |
) = |  |∙|
|∙|  | cos90 = 0.
| cos90 = 0.
Если (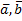 ) = 0 => векторы перпендикулярны, т.к. cos90 = 0.
) = 0 => векторы перпендикулярны, т.к. cos90 = 0.
Свойства векторного произведения (доказать) и его геометрический смысл.
Векторным произведением двух ненулевых векторов  и
и  называется вектор
называется вектор 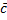 , удовлетворяющий следующим условиям:
, удовлетворяющий следующим условиям:
1) | 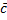 | = |
| = |  | × |
| × |  | × sinj, где j – угол между векторами
| × sinj, где j – угол между векторами  и
и  ;
;
2) вектор 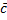 ортогонален векторам
ортогонален векторам  и
и  ;
;
3) тройка векторов  ,
,  и
и 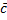 – правая.
– правая.
Если хотя бы один из векторов  или
или  нулевой, то их векторное произведение полагают равным нулевому вектору. (Об: [
нулевой, то их векторное произведение полагают равным нулевому вектору. (Об: [  ,
,  ] или
] или  ´
´  .)
.)
Свойства векторного произведения:
1) При перестановке векторов  и
и  их векторное произведение меняет знак, т.е. [
их векторное произведение меняет знак, т.е. [  ,
,  ] = – [
] = – [  ,
,  ].
].
Векторы [  ,
,  ] и [
] и [  ,
,  ] коллинеарны, имеют одинаковые модули, но противоположно направлены (тройки
] коллинеарны, имеют одинаковые модули, но противоположно направлены (тройки  ,
,  , [
, [  ,
,  ] и
] и  ,
,  , [
, [  ,
,  ] противоположной ориентации). Значит, [
] противоположной ориентации). Значит, [  ,
,  ] = – [
] = – [  ,
,  ].
].
2) Числовой множитель любого из двух векторов можно вынести за знак векторного произведения, т.е. [ l  ,
,  ] = [
] = [  , l
, l  ] = l [
] = l [  ,
,  ].
].
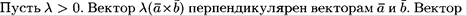

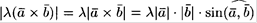
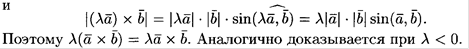
3) Если один из векторов записан в виде суммы, то векторное произведение тоже можно записать в виде суммы. А именно: [  1 +
1 +  2,
2,  ] = [
] = [  1,
1,  ] + [
] + [  2,
2,  ][
][  ,
,  1 +
1 +  2 ] = [
2 ] = [  ,
,  1 ] + [
1 ] + [  ,
,  2 ].
2 ].
4) Критерий коллинеарности векторов.
Ненулевые векторы  и
и  коллинеарные Û их векторное произведение равно нулевому вектору.
коллинеарные Û их векторное произведение равно нулевому вектору.
5) Геометрический смысл векторного произведения.
Модуль векторного произведения неколлинеарных векторов  и
и  равен площади параллелограмма, построенного на этих векторах.
равен площади параллелограмма, построенного на этих векторах.
6) Если в декартовом прямоугольном базисе векторы  и
и  имеют координаты:
имеют координаты:  = { ax; ay; az },
= { ax; ay; az },  = { bx; by; bz }, то
= { bx; by; bz }, то
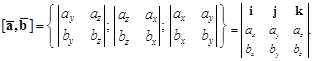 |
7) Механический смысл векторного произведения.
Если вектор 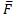 это сила, приложенная к точке M, то векторное произведение [
это сила, приложенная к точке M, то векторное произведение [ 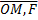 ] представляет собой момент силы
] представляет собой момент силы 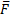 относительно точки O.
относительно точки O.
Критерий коллинеарности векторов (с док-ом, используя векторное произведение векторов).
Ненулевые векторы  и
и  коллинеарные Û их векторное произведение равно нулевому вектору.
коллинеарные Û их векторное произведение равно нулевому вектору.
Если  ||
||  , то угол м/у ними равен 0 или 180.
, то угол м/у ними равен 0 или 180.
Но тогда [  ,
,  ] = |
] = |  | × |
| × |  | × sin(
| × sin(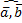 ) = 0. Значит, [
) = 0. Значит, [  ,
,  ] = 0.
] = 0.
Если же [  ,
,  ] = 0, то |
] = 0, то |  | × |
| × |  | × sinj= 0. Но тогда j = 0 или j = 180, т.е.
| × sinj= 0. Но тогда j = 0 или j = 180, т.е.  ||
|| 
Вычисление векторного произведения в декартовой системе координат (с выводом формулы).
Пусть известны координаты векторов 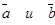 , то есть
, то есть
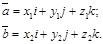
Используя свойства векторного произведения, найдем:
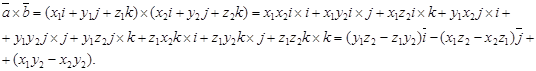
Выражения в скобках можно записать с помощью определителей второго порядка (проверьте), то есть:
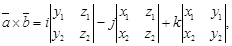
правую часть последнего выражения можно записать с помощью определителя третьего порядка:
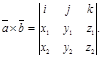
Эта формула является удобной записью векторного произведения в координатах.
Смешанное произведение трёх векторов: определение и свойства (доказать).
ОПРЕДЕЛЕНИЕ: Смешанным произведением трех векторов ā, b̄ и c̄ называется число, равное скалярному произведению вектора ā на векторное произведение векторов b̄ и c̄, т.е.
(ā, [ b̄, с̄ ]).
Обозначают: (ā, b̄, с̄) или ā b̄ с̄.
Свойства смешанного произведения
Если a,b,c и d — произвольные векторы, а t — произвольное число, то:
1) (a,b,c) = (b,c,a) = (c,a,b) = −(a,c,b) = −(c,b,a) = −(b,a,c);
2) (ta,b,c) = (a,tb,c) = (a,b,tc) = t · (a,b,c);
3) (a + b,c,d) = (a,c,d) + (b,c,d) (смешанное произведение дистрибутивно относительно сложения векторов по первому
аргументу); (a,b + c,d) = (a,b,d) + (a,c,d) (смешанное произведение дистрибутивно относительно сложения векторов по второму
аргументу); (a,b,c + d) = (a,b,c) + (a,b,d) (смешанное произведение дистрибутивно относительно сложения векторов по третьему аргументу).
5)Если смешанное произведение векторов а, b, c положительно, то векторы а, b, c образуют правую тройку. Иначе векторы а, b, c образуют левую тройку
Критерий компланарности трёх векторов (доказать).
Критерий компланарности векторов
Векторы a,b и c компланарны тогда и только тогда, когда их смешанное
произведение равно нулю.
Date: 2015-09-05; view: 732; Нарушение авторских прав