
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Скалярное произведение векторов
|
|
Критерий линейной зависимости трёх векторов
Три свободных вектора линейно зависимы Û они компланарны.
Доказательство:
1) Необходимость. Пусть векторы 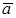 ,
, 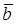 и
и  – линейно зависимы. Тогда по определению существуют числа
– линейно зависимы. Тогда по определению существуют числа  (хотя бы одно из них отличное от нуля) такие, что выполняется равенство
(хотя бы одно из них отличное от нуля) такие, что выполняется равенство  . Пусть, например,
. Пусть, например, 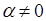 .
.
Тогда 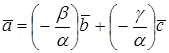 . Следовательно,
. Следовательно, 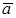 ,
, 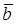 и
и  лежат в одной плоскости, т.е. они компланарны.
лежат в одной плоскости, т.е. они компланарны.
2) Достаточность. Пусть 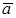 ,
, 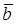 и
и  – компланарны. Рассмотрим 2 случая.
– компланарны. Рассмотрим 2 случая.
а) Пусть 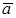 ||
|| 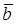 . Тогда
. Тогда 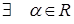 такое, что выполняется равенство
такое, что выполняется равенство  . Тогда
. Тогда 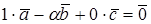 . Следовательно, векторы
. Следовательно, векторы 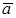 ,
, 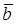 и
и  – линейно зависимы.
– линейно зависимы.
б) Пусть 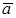 и
и 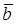 не параллельны. Тогда
не параллельны. Тогда 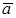 и
и 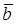 образуют базис. Следовательно, вектор
образуют базис. Следовательно, вектор  можно представить в виде линейной комбинации базисных векторов. Тогда векторы
можно представить в виде линейной комбинации базисных векторов. Тогда векторы 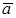 ,
, 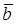 и
и  – линейно зависимы.
– линейно зависимы.
Скалярное произведение векторов: определение и свойства (доказать).
Скалярное произведение векторов
Скалярным произведением двух ненулевых векторов 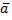 и
и  называется число, равное произведению модулей этих векторов на косинус угла между ними, т.е. число
называется число, равное произведению модулей этих векторов на косинус угла между ними, т.е. число 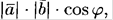
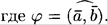
Если  = 0 или
= 0 или  = 0, то скалярное произведение векторов полагают равным нулю.
= 0, то скалярное произведение векторов полагают равным нулю.
Date: 2015-09-05; view: 507; Нарушение авторских прав