Обратное преобразование Лапласа

Обратным преобразованием Лапласа называется преобразование изображения в оригинал.

Если изображение 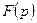, то его оригинал 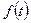в общем случае определяется формулой Римана-Меллина

.

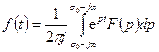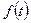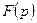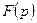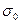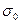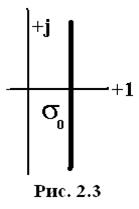
Преобразование, осуществляемое этой формулой, т.е. нахождение по известному , называется обратным преобразованием Лапласа. Чтобы осуществить это преобразование нужно найти особые точки (полюса, точки ветвления функции) и взяв так, чтобы все особые точки легли левее прямой , произвести интегрирование вдоль прямой 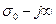, 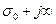(рис. 2.3).

Во многих простейших случаях для нахождения оригиналов можно использовать табличные данные (табл. 2.1).

Таблица 2.1

Оригинал	Изображение

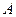
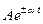
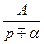
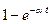
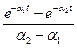
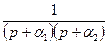
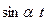
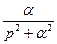
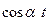
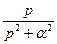
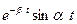
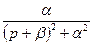
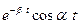
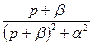
В тех случаях, когда 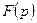представляет рациональную дробь, проще пользоваться так называемой теоремой разложения, которая вытекает из формулы Римана-Меллина. Суть этой теоремы: сложная рациональная дробь разлагается на простые дроби, оригиналы которых известны.

Докажем эту теорему, не прибегая к формуле Римана-Меллина.

Пусть

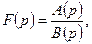
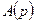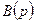где и - полиномы, которые определяются следующим образом:

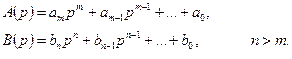
Внимание, степени у членов полинома должны быть натуральными числами или равняться нулю, если в ходе решения получены отрицательные степени, необходимо и числитель и знаменатель умножить на одно и тоже число, чтобы отрицательные степени исчезли.

Предположим, что уравнение 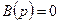имеет только простые корни (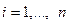), т.е. особыми точками функции 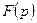являются полюса. Все 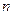корней идентичны корням характеристического уравнения, различие может быть только в постоянном множителе и в появлении нулевого корня.

Разложим рациональную дробь 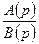на простейшие дроби:

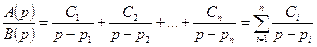, (2.5)

где 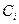- постоянные коэффициенты. Они определяются следующим образом. Умножим (2.5) на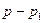

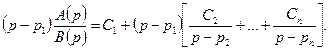
Положим 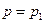. Тогда второй член в правой части исчезает, в левой части имеем неопределенность типа 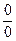, т.к. 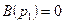. Раскроем эту неопределенность по правилу Лапиталя:

,

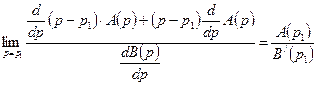где , .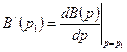

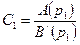Аналогично получаем

.

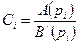Таким образом,

.

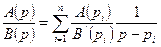Известно, что

.

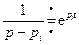Следовательно, изображению 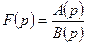соответствует оригинал 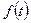, равный

.

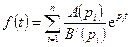Эта формула определяет теорему разложения.

Допустим, что один из корней уравнения 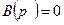равен нулю, т.е. знаменатель можно представить так: 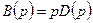и .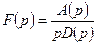

Тогда по теореме разложения имеем:

,

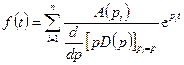знаменатель можно представить следующим образом:

.

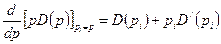Нулевой корень обозначим 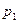, тогда при 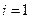второе слагаемое исчезает, при 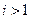исчезает первый член и теорему разложения можно представить в виде:

.

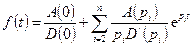Важное значение при нахождении оригинала имеет теорема свертывания или теорема Бореля. Она заключается в следующем. Пусть изображение 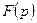представимо в виде 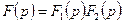и пусть известно, что 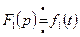и 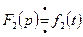. Тогда если 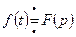, то 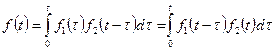. Т.е. 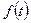определяется как свертка 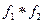. Под сверткой двух функци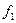й и 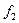, ее обозначают 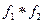, понимают интеграл .

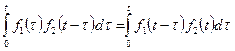Понятие об интеграле свертки может быть положено в основу нескольких полезных соотношений, из которых интеграл Дюамеля является наиболее известным.

Эту теорему можно использовать, когда уравнение 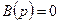имеет кратные корни.

Пример.

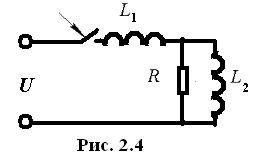
Рассмотрим включение цепи (рис. 2.4) при нулевых начальных условиях.

Операторное сопротивление равно:

.

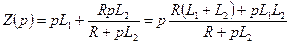Операторный ток равен: 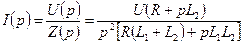. В знаменателе имеется кратный корень 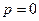. Применим теорему свертывания 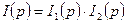, где

,

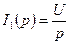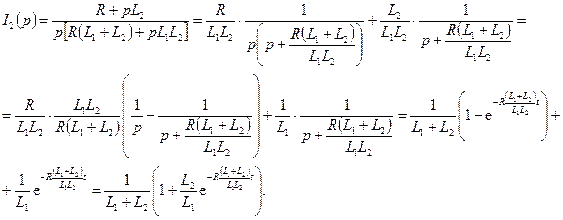
Найдем оригиналы токов:

, ,

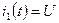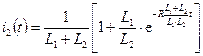а затем оригинал тока в общей ветви:

.

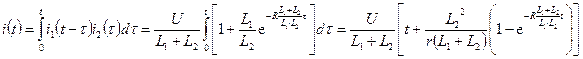Допустим, что 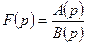и пусть степени полиномов 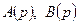одинаковы. Представим 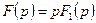и пусть 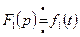. Тогда 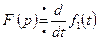. Такой случай встречается при расчете напряжения на индуктивности.

Допустим, что 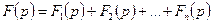и пусть 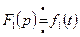, ,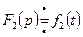…, 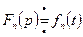. Тогда .

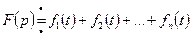Date: 2015-09-17; view: 1319; Нарушение авторских прав