Законы Кирхгофа в операторной форме

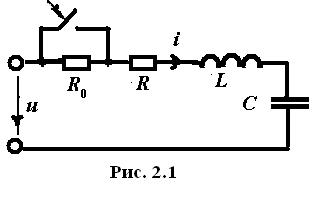Уравнения электрической цепи, составленные для изображений, называются операторными уравнениями цепи. Для их составления применяются законы Кирхгофа в операторной форме.

I закон Кирхгофа

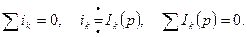
II закон Кирхгофа

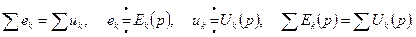
При составлении уравнений Кирхгофа в операторной форме нужно соблюдать все правила знаков, которые были установлены при составлении уравнений Кирхгофа для оригиналов - фактических токов и напряжений.

Все операторные токи, отходящие от узла записываются со знаком «-», в противном случае со знаком «+». Задавшись направлениями токов, ЭДС и обхода контура, приписывают току, падению напряжения и ЭДС знак «+», если их направления совпадают с направлением обхода, в противном случае – знак «-».

Пусть имеется цепь (рис. 2.1). Необходимо определить переходный ток.

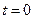- момент коммутации. При 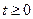имеем

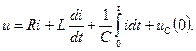
Перейдем к изображениям

, .

,

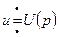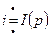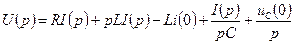где 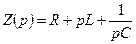- операторное сопротивление данной цепи.

Отсюда находим операторный ток:

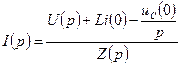. (2.3)

Выражение (2.3) это закон Ома, записанный для переходного процесса при ненулевых начальных условиях. Если имеются нулевые начальные условия, то закон Ома имеет вид

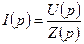. (2.4)

Сопоставляя формулы (2.3) и (2.4) видим, что в случае ненулевых начальных условий операторный ток равен сумме операторного тока, обусловленного приложенным к цепи напряжением, и операторного тока, вызываемого добавочной ЭДС, определяемой ненулевыми начальными условиями.

Из рассмотренного примера видно, как записывается операторное изображение отдельных параметров цепи.

Операторное изображение активного сопротивления есть само активное сопротивление .

Операторное индуктивное сопротивление определяется следующим образом: .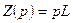

Операторное емкостное сопротивление равно: .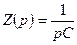

Рассмотрим два предельных случая.

1). Для постоянного тока сопротивление рассматриваемой цепи равно 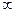, т.к. имеется конденсатор и ток равен нулю. Если 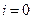, то 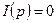, поэтому 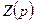должно равняться 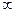. Это возможно, если 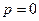. Таким образом, операторное сопротивление цепи в случае постоянного тока получается в предположении 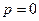в формуле операторного сопротивления, составленной для общего случая.

2). Если по цепи протекает синусоидальный ток частоты 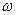и постоянной амплитуды, то сопротивление цепи равно 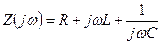. Следовательно, сопротивление цепи синусоидальному току можно получить, полагая 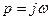в выражении для операторного сопротивления.

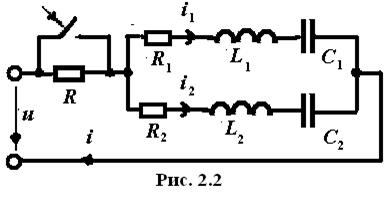
Рассмотрим более сложную цепь (рис. 2.2).

Перейдем к изображениям:

, , ,

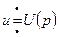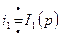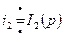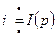
Запишем уравнения цепи:

,

,

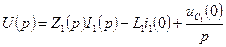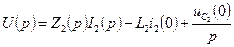где операторные сопротивления ветвей равны:

, .

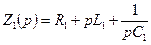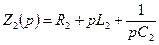Операторный ток согласно I закону Кирхгоффа равен:

.

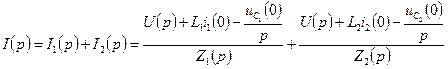Величины, обратные операторным сопротивлениям, называются операторными проводимостями: .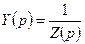

Операторный ток в общей ветви равен:

.

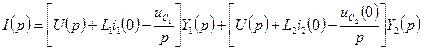При нулевых начальных условиях выражение упрощается:

.

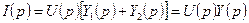Таким образом, преобразование Лапласа позволяет перейти от дифференциальных уравнений цепи к операторным уравнениями, которые записываются в алгебраической форме. Как видно в результате решения этих уравнений получаем лишь изображения исходных величин. Перед расчетчиком возникает вторая задача, как от изображений перейти к оригиналам. Это можно сделать, используя обратное преобразование Лапласа.

Date: 2015-09-17; view: 1117; Нарушение авторских прав