Преобразования Фурье

В случае линейных электрических цепей, когда напряжение или ЭДС, действующие в них несинусоидальные и представляют периодические функции времени и эти функции удовлетворяет условиям Дирихле, расчет токов осуществляется путем разложения напряжений или ЭДС в ряд Фурье. Искомый ток определяется как сумма отдельных гармоник тока, причем каждая из этих гармоник отыскивается независимо от других в предположении, что в цепи действует только соответствующая гармоника напряжения или ЭДС.

Возникает вопрос о возможности подобного решения в случае непериодических напряжений и токов, как это имеет место при переходном процессе. Оказывается это возможно, если вместо ряда Фурье использовать интеграл Фурье.

Для получения интеграла Фурье необходимо предварительно рассмотреть ряд Фурье в комплексной форме:

, .

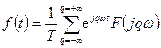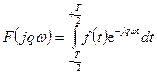где 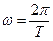- угловая частота первой гармоники.

Используя формулы Эйлера: 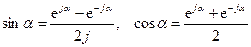, получим

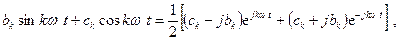
но 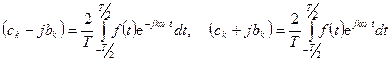, тогда

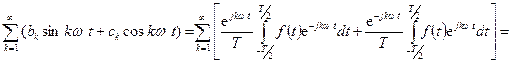
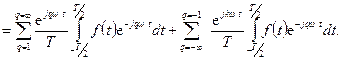
Замена в первой сумме 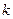на 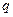, а во второй сумме 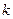на - 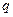была сделана, чтобы получить одинаковые выражения под знаками обеих сумм.

Так как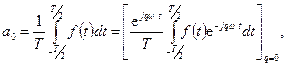

то , 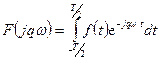. (3.1)

Формулы (3.1) описывают ряд Фурье в комплексной форме.

Обозначим частоту первой гармоники 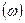как 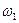( 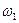- фиксированная величина, 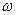- переменная величина). Перепишем формулы (3.1) в виде

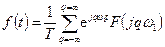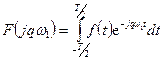, . (3.2)

Здесь k -ой гармонике отвечает сумма двух сопряженных членов ().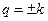

Частоты любых соседних гармоник отличаются на одну и ту же (конечную) величину 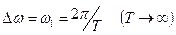. Таким образом, частоты гармоник в ряде Фурье образуют дискретный спектр.

Пусть 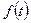- непериодическая функция. Будем рассматривать ее как периодическую, но с бесконечно большим периодом. При этом разность частот соседних гармоник 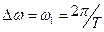стремится к нулю, и дискретный спектр частот превращается в непрерывно изменяющуюся частоту.

Из формулы (3.2) получим

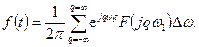
Отсюда при 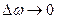имеем

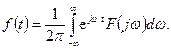(3.3)

Т.е. ряд Фурье переходит в интеграл Фурье. Соответственно

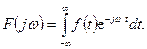(3.4)

Формула (3.4) называется прямым преобразованием Фурье. Оно позволяет найти 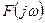по заданной 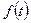. Формула (3.3) называется обратным преобразованием Фурье. Оно позволяет найти 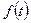по известной .

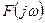Если при 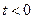(например, ЭДС, включаемая на цепь при 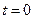), то формула (3.4) получает вид

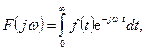
которое называется односторонним прямым преобразованием Фурье.

Прямое преобразование Фурье имеет смысл, если существует интеграл 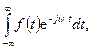т.е. когда он конечен. Для этого необходима и достаточна абсолютная интегрируемость 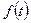в пределах 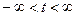, т.е. должен существовать интеграл 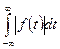. Это, как правило, означает, что 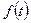должен стремиться к нулю при .

Между односторонним преобразованием Фурье

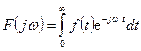
и преобразованием Лапласа

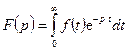
существует связь. Т.е. одностороннее прямое преобразование Фурье лишь частный случай преобразования Лапласа при 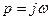. Иными словами, если известно операторное изображение 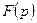некоторой функции 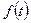, то одностороннее прямое преобразование Фурье получаем, полагая 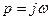в формуле для .

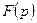Date: 2015-09-17; view: 475; Нарушение авторских прав