Соединенными R и L (контуры 1 порядка)

А). Включение на постоянное напряжение (Рис. 1.1).

Здесь и в дальнейшем направление стрелки у ключа показывает действие во время коммутации. Пусть t= 0 есть момент коммутации. Составим уравнение цепи после коммутации ()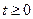

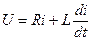. (1.5)

Решение уравнения (1.5) ищем в виде

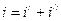. (1.6)

Установившийся ток нового стационарного режима равен .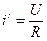

Свободный ток ищем в виде

.

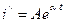Составим уравнение для свободного тока, для этого в уравнении (1.5) приравняем нулю приложенное напряжение, в результате получим

.

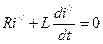Характеристическое уравнение имеет вид

.

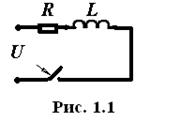
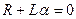Решаем характеристическое уравнение и находим корень:

.

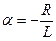Величина 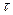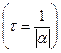называется постоянной времени, она характеризует интенсивность протекания переходного процесса. Теоретически новый установившийся режим наступает при 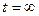. Практически уже при 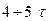переходный процесс можно считать завершенным.

Внимание. Обычно длительность переходных процессов можно считать измеряемой долями секунд. В цепях, не содержащих индуктивных катушек и конденсаторов, установившийся режим наступает практически мгновенно.

Чтобы найти постоянную интегрирования А, уравнение (7) запишем следующим образом:

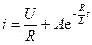. (1.7)

До коммутации (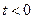) ток в цепи определяется следующим образом .

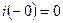Согласно закону коммутации .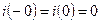

Запишем уравнение (1.7) для момента коммутации 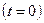и найдем величину А

, .

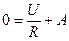Формируем выражение для тока в переходном режиме в соответствии с формулой (1.7):

.

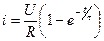Задаваясь значениями времени по полученному выражению можно построить график тока (рис. 1.2). При этом необходимо учитывать, что переходный процесс, как правило, длится 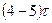. Постоянную 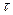можно определить по графикам. Для этого необходимо провести касательную к любой точки графика, опустить перпендикуляры на ось времени из точки касания и точки пересечения касательной уровня, соответствующего установившемуся значению тока. Расстояние между этими перпендикулярами равно постоянной времени.

Напряжение на индуктивности определяется по формуле:

.

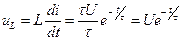По аналогии строится график изменения напряжения на индуктивной катушке во время переходного режима (рис. 1.2).

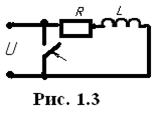
Б). Короткое замыкание (Рис. 1.3).

Пусть t= 0 есть момент коммутации. Составим уравнение цепи после коммутации ()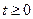

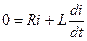. (1.8)

Решение уравнения (1.8) ищем в виде

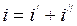. (1.9)

Установившийся ток нового стационарного режима равен .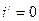

Свободный ток ищем в виде

.

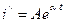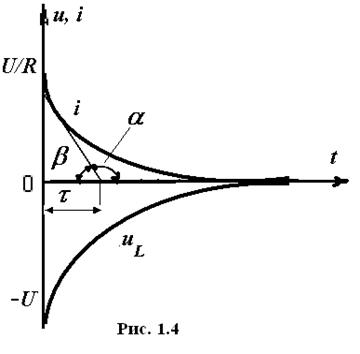Составим уравнение для свободного тока:

.

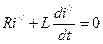Характеристическое уравнение имеет вид

.

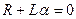Корень характеристического уравнения равен

.

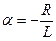Выражение для постоянной времени имеет вид:

.

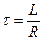Чтобы найти постоянную интегрирования А, уравнение (1.9) запишем следующим образом:

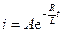, (1.10)

До коммутации (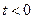) ток в цепи определяется следующим образом:

.

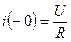Согласно закону коммутации

.

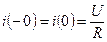Запишем уравнение (1.10) для момента коммутации и найдем величину А:

.

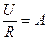Выражение для тока в переходном режиме выглядит следующим образом:

.

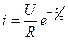Задаваясь значениями времени по полученному выражению можно построить график тока (рис. 1.4).

По аналогии строится график изменения напряжения на индуктивности во время переходного режима (рис. 1.4)

.

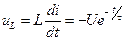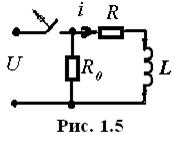
В) Отключение цепи (Рис. 1.5).

Пусть t= 0 есть момент коммутации. Составим уравнение цепи после коммутации ()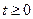

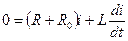. (1.11)

Решение уравнения (1.11) ищем в виде:

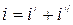. (1.12)

Установившийся ток нового стационарного режима равен .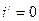

Свободный ток ищем в виде

.

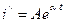Составим уравнение для свободного тока, пользуясь уравнением (1.11):

.

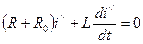Характеристическое уравнение имеет вид:

.

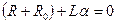Корень характеристического уравнения равен 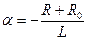. Тогда постоянная времени равна

.

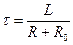Чтобы найти постоянную интегрирования А, уравнение (1.12) запишем следующим образом:

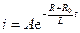. (1.13)

До коммутации ток в цепи определяется следующим образом .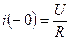

Согласно закону коммутации:

.

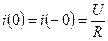Запишем уравнение (1.13) для момента коммутации и найдем величину А

, .

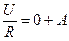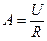Выражение для тока в переходном режиме выглядит следующим образом:

.

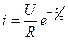Задаваясь значениями времени по полученному выражению можно построить график тока (не приводится).

Напряжение на 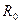до коммутации равно 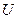. При 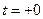стало:

.

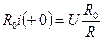Если 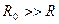, то напряжение на 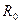при отключении цепи велико. Поэтому обмотки возбуждения электрических машин (они имеют большую L) снабжаются аппаратами гашения поля. Эти аппараты предохраняют обмотку возбуждения от электрического пробоя.

Г). Включение на синусоидальное напряжение .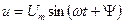

Пусть t= 0 есть момент коммутации. Составим уравнение цепи после коммутации ()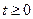

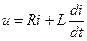. (1.14)

Решение уравнения (1.14) ищем в виде:

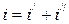. (1.15)

Установившийся ток нового стационарного режима равен

,

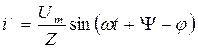где , .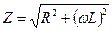

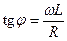Свободный ток ищем в виде

.

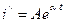Составим уравнение для свободного тока, для этого в уравнении (1.14) приравняем нулю приложенное напряжение, в результате получим:

.

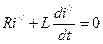Характеристическое уравнение имеет вид:

.

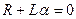Корень характеристического уравнения равен 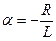. Отсюда найдем постоянную времени: .

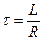Чтобы найти постоянную интегрирования А, уравнение (1.15) запишем следующим образом:

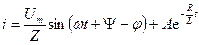. (1.16)

До коммутации ток в цепи равен .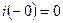

Согласно закону коммутации:

.

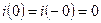Запишем уравнение (1.16) для момента коммутации 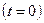и найдем величину А:

, .

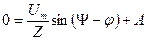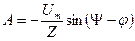Формируем выражение для тока в переходном режиме:

.

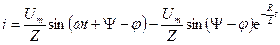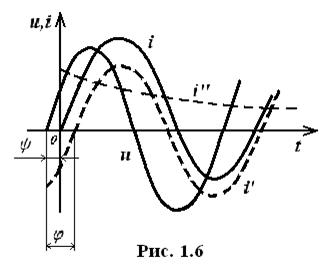Задаваясь значениями времени по полученному выражению можно построить график тока (рис. 1.6).

Начальное значение свободного тока зависит от 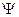(фазы включения). Он принимает максимальное значение при .

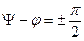Наибольшее значение результирующего тока не превышает удвоенной амплитуды установившегося тока.

Date: 2015-09-17; view: 419; Нарушение авторских прав