
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Теорема 3. (свойство углов равнобедренного треугольника)
|
|
В равнобедренном треугольнике углы при основании равны.
| ▩ Пусть ABC — равнобедренный треугольник с основанием АВ (рис. 3). Докажем, что у него ∠А = ∠В. Треугольник CAB равен треугольнику СВА по первому признаку равенства треугольников. Действительно, СА = СВ, СВ = СА, ∠С = ∠С. Из равенства треугольников следует, что ∠А = ∠В. ▩ | 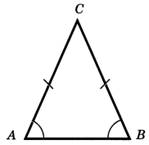 Рис. 3
Рис. 3
|
ТЕОРЕМА 4. (СВОЙСТВО МЕДИАНЫ РАВНОБЕДРЕННОГО ТРЕУГОЛЬНИКА).
В равнобедренном треугольнике медиана, проведенная к основанию, является биссектрисой и высотой.
| ▩ Пусть ABC — данный равнобедренный треугольник с основанием АВ и CD — медиана, проведенная к основанию (рис. 4). Треугольники CAD и CBD равны по первому признаку равенства треугольников (Т. 1). У них стороны АС и ВС равны, потому что треугольник ABC равнобедренный. Углы CAD и CBD равны как углы при основании равнобедренного треугольника. Стороны AD и BD равны, потому что D — середина отрезка АВ. Из равенства треугольников следует равенство углов: ∠ACD = ∠BCD, ∠ADC = ∠BDC. Так как углы ACD и BCD равны, то CD — биссектриса. Так как углы ADC и BDC смежные и равны, то они прямые, поэтому CD — высота треугольника. ▩ | 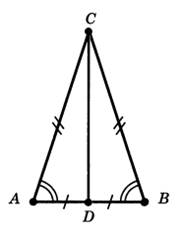 Рис. 4
Рис. 4
|
Date: 2015-09-05; view: 1203; Нарушение авторских прав