
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Классификация точек разрыва функции
|
|
Все точки разрыва функции разделяются на точки разрыва первого и второго рода.
Говорят, что функция f (x) имеет точку разрыва первого рода при x = a, если в это точке
- Существуют левосторонний предел
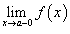 и правосторонний предел
и правосторонний предел 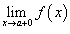 ;
; - Эти односторонние пределы конечны.
При этом возможно следующие два случая:
- Левосторонний предел и правосторонний предел равны друг другу:
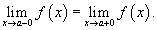
Такая точка называется точкой устранимого разрыва.
- Левосторонний предел и правосторонний предел не равны друг другу:
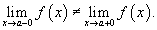
Такая точка называется точкой конечного разрыва. Модуль разности значений односторонних пределов  называется скачком функции.
называется скачком функции.
Функция f (x) имеет точку разрыва второго рода при x = a, если по крайней мере один из односторонних пределов не существует или равен бесконечности.
Пример 3.13 Рассмотрим функцию 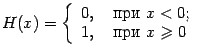 (функция Хевисайда) на отрезке
(функция Хевисайда) на отрезке 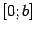 ,
, 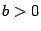 . Тогда
. Тогда 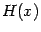 непрерывна на отрезке
непрерывна на отрезке 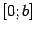 (несмотря на то, что в точке она имеет разрыв первого рода).
(несмотря на то, что в точке она имеет разрыв первого рода).
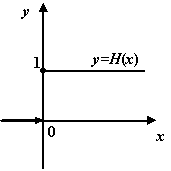
Рис.3.15.График функции Хевисайда
Аналогичное определение можно дать и для полуинтервалов вида 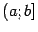 и
и 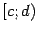 , включая случаи
, включая случаи 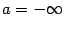 и
и 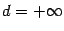 . Однако можно обобщить данное определение на случай произвольного подмножества
. Однако можно обобщить данное определение на случай произвольного подмножества 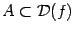 следующим образом. Введём сначала понятие индуцированной на базы: пусть -- база, все окончания которой имеют непустые пересечения с. Обозначим
следующим образом. Введём сначала понятие индуцированной на базы: пусть -- база, все окончания которой имеют непустые пересечения с. Обозначим 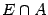 через
через 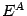 и рассмотрим множество всех
и рассмотрим множество всех 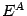 . Нетрудно тогда проверить, что множество
. Нетрудно тогда проверить, что множество 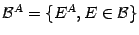 будет базой. Тем самым для
будет базой. Тем самым для 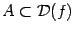 определены базы
определены базы 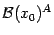 ,
, 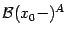 и
и 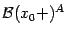 , где
, где 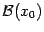 ,
, 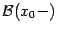 и
и 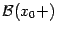 -- базы непроколотых двусторонних (соответственно левых, правых) окрестностей точки
-- базы непроколотых двусторонних (соответственно левых, правых) окрестностей точки 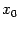 (их определение см. в начале текущей главы).
(их определение см. в начале текущей главы).
38. Производная. Её геометрический смысл. Дифференцируемость функции.
Пусть 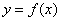 - функция,
- функция, 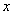 - произвольная (но фиксированная) точка из области её определения.
- произвольная (но фиксированная) точка из области её определения.
Производной функции 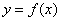 в точке
в точке 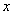 называется предел (если он существует и конечен) отношения приращения функции к приращению аргумента при условии, что последнее стремится к нулю.
называется предел (если он существует и конечен) отношения приращения функции к приращению аргумента при условии, что последнее стремится к нулю.
Наиболее употребительны следующие обозначения производной:
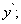
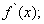
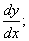
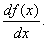
Геометрический смысл производной – производная от данной функции f(x) при данном
значении x0 аргумента равна угловому коэффициенту касательной к графику этой
функции в соответствующей точке M0(x0, f(x0)).
Date: 2015-09-05; view: 542; Нарушение авторских прав