Доказательство. 1) Существование общей точки

1) Существование общей точки. Множество левых концов отрезков {a_n} лежит на числовой прямой левее множества правых концов отрезков {b_n}, поскольку

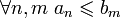
В силу аксиомы непрерывности, существует точка c, разделяющая эти два множества, то есть

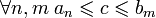
в частности

Последнее неравенство означает, что c — общая точка всех отрезков данной системы.

2) Единственность общей точки. Пусть длина отрезков системы стремится к нулю. Покажем, что существует только одна точка, принадлежащая всем отрезкам системы. Предположим противное: пусть имеется две различные точки c и c', принадлежащие всем отрезкам системы:

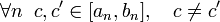
Тогда для всех номеров n выполняются неравенства:

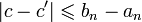
В силу условия стремления к нулю длин отрезков для любого для всех номеров n, начиная с некоторого будет выполняться неравенство

b_n − a_n < ε

Взяв в этом неравенстве 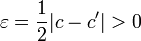, получим

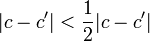
Противоречие. Лемма доказана полностью.

24.Бесконечно большая последовательность

Определение. Последовательность {x_n} называется бесконечно большой, если для любого положительного числа A можно указать номер N такой, что при 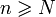все элементы x_n этой последовательности удовлетворяют неравенству .

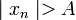Любая бесконечно большая последовательность является неограниченной. Но не каждая неограниченная последовательность является бесконечно большой. Например, неограниченная последовательность 1, 2, 1, 3,... 1, n,... не является бесконечно большой, так как при A > 1 неравенство 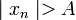не выполняется для x_n с нечетными номерами.

Бесконечно малая последовательность

Определение. Последовательность {x_n} называется бесконечные малой, если для любого положительного числа ε можно указать номер N такой, что при 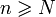все элементы x_n этой последовательности удовлетворяют неравенству .

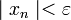Любая бесконечно малая последовательность является ограниченной

Date: 2015-09-05; view: 404; Нарушение авторских прав