Неперервність функції в точці і на проміжку

Функція називається неперервною в точці 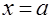, якщо границя функції в цій точці існує і дорівнює значенню функції в цій точці .

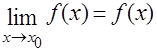Умови неперервності функції в точці:

1. Границя функції 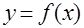в точці 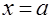визначена.

2. Границя функції 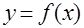в точці 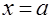існує.

3. Границя дорівнює значенню функції в цій точці.

Функція називається неперервною проміжку, якщо вона неперервна в кожній точці цього проміжку.

Властивості неперервних функцій:

1. Якщо функції f (x) і g (x) неперервні в точці a, то сума, добуток і частка неперервних в точці a функцій неперервні в точці a (частка у випадку, коли дільник g (a) ≠ 0).

2. Графік функції, неперервної на проміжку, — нерозривна лінія на цьому проміжку.

3. Всі елементарні функції неперервні в кожній точці своєї області визначення, тому на кожному проміжку з області визначення їх графіки — нерозривні лінії.

3. Многочлен є функція неперервна на всій числовій осі.

4. Дробово-раціональна функція є функція неперервна на області визначення.

5. Якщо функція 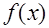неперервна на сегменті 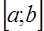, то вона на цьому сегменті обмежена.

6. Якщо функція 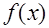неперервна на сегменті 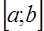, то вона на цьому сегменті приймає найменше і найбільше значення.

7. Якщо функція 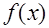непевна на сегменті 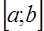і на його кінцях приймає значення різних знаків, то існує хоч би одна точка С на 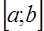, в якій .

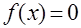Date: 2015-09-05; view: 713; Нарушение авторских прав