Ориентирование линий

Ориентировать линию - значит определить ее направление относительно меридиана. Вообразим в данной точке земной поверхности отвесную линию; плоскость, проходящая через эту отвесную линию и ось вращения Земли, называется плоскостью географического или истинного меридиана в данной точке.

С(О')

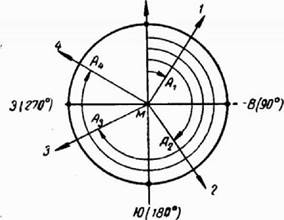
Рис. 19. Углы ориентирования

Направление истинного меридиана определяется на данной точке при помощи астрономических наблюдений, а направление магнитного меридиана - при помощи магнитной стрелки, которая устанавливается под действием земного магнетизма в направлении магнитного меридиана. Конец стрелки, обращенный северному полюсу Земли, называют северным, а другой конец - южным. Магнитный меридиан в данной точке земной поверхности, как правило, не совпадает с истинным: угол между ними называется склонением магнитной стрелки. Склонение называют восточным или западным, смотря по тому, отклоняется ли северный конец магнитной стрелки к востоку или к западу от географического меридиана.

Для ориентирования линий служат углы ориентирования, называемые азимутами, дирекционными углами и румбами.

Азимуты. Азимутом называется горизонтальный угол, отсчитываемый от северного направления меридиана по ходу часовой стрелки до направления данной линии; азимуты могут иметь значения от 0 до 360°. Азимут называется истинным, если он отсчитывается от истинного меридиана, и магнитным, если он отсчитывается от магнитного меридиана.

Пусть линия СЮ (рис. 19) — направление меридиана в точке М (истинного или магнитного). 3В - направление, перпендикулярное к меридиану. Тогда направление МВ укажет на восток, а МЗ — на запад.

Рассмотрим проекции линий местности М1, М2, МЗ и М4 на горизонтальную плоскость. Горизонтальные углы А_1г А₂,, Аз и А₄ представят азимуты этих линий. Если линия СЮ есть истинный меридиан, то и азимуты этих линий будут истинными азимутами. Если же СЮ - магнитный меридиан, то эти углы - магнитные азимуты.

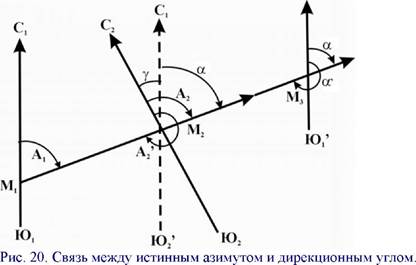
Так как меридианы в разных точках Земли не параллельны между собой, то азимут одной и той же линии в разных ее точках различен. Так, для линии М₁М₂ (рис. 20) азимут в точке М₁ равен А_ь в точке М₂—А₂; азимут А₂ отличается от азимута А₁ на величину угла у между меридианами этих точек. Этот угол у называется сближением меридианов. Его легко представить, если провести мысленно через одну из двух данных точек направление, параллельное меридиану другой точки. На рис. 20 угол у представлен как угол между меридианом С₂Ю₂ точки М₂ и направлением С Ю1 ЦС1 Ю_ь

Как видно из рисунка,

А - А = у.

Если точки М₁ и М₂ близки, то можно принять у=0, и тогда А₂=А₁, а меридианы в соответствующих точках можно рассматривать как параллельные.

Азимут данного направления называется прямым, а противоположного - обратным.

Для линии М₁М₂ (рис. 20) А₁ и А₂—прямые азимуты этой линии в разных ее точках, А₂ - обратный азимут той же линии в точке М₂.

Как видно на рис. 20,

а; = а +180⁰ + у (IV. 1)

а; = А₂ +180⁰, (IV.;)

т. е. прямой и обратный азимуты одной и той же линии в разных ее точках отличаются между собой на 180°+ у; прямой и обратный азимуты данной линии в одной и той же точке различаются на 180°.

Дирекционные углы. Дирекционные углы применяются в геодезии для ориентирования линий относительно осевого меридиана, или линии, ему параллельной. Если на рис. 20 меридиан С1Ю1 точке М1 будем рассматривать как осевой в равноугольной поперечно-цилиндрической проекции, линию С₂Ю₂ как истинный, меридиан в точке М₂, а линию С Ю1, параллельную С1Ю1, как одну из вертикальных линий километровой сетки, то А2 представит истинный азимут, а а - дирекционный угол линии М₁М₂ в точке М₂, т. е. дирекционный угол отсчитывается от северного направления осевого меридиана или линии, ему параллельной, по ходу часовой стрелки до направления данной линии в пределах 0 - 360°. Из рисунка видно, что

А₂ - а = у, (а)

т. е. разность между истинным азимутом и дирекционным углом какой-нибудь линии в данной на ней точке равна сближению истинного меридиана в этой точке с осевым меридианом зоны.

Из формулы (а) находим, что

А₂ =а + у. (гу\3.)

На рис. 20 точка М₂ была взята восточное осевого меридиана. Если же точка М₂ расположена западнее осевого меридиана С1Ю1 (рис. 22), тогда

А; = а - у.

Но обыкновенно сближение меридианов для точек, расположенных к западу от осевого меридиана, выражают числом отрицательным. Тогда формула (ГУ.3) будет общей для обоих случаев.

В отличие от азимута А дирекционный угол а (рис. 20) одной и той же линии в разных ее точках остается постоянным; в точке М₃ он будет такой же, как и в точке М₂.

На небольших участках, когда по малости величиной у можно пренебречь и меридианы в различных точках рассматривать как параллельные между собой, то один из них, с которым совмещают ось абсцисс произвольной системы прямоугольных координат, принимается за осевой меридиан. В таких случаях направления линий определяются дирекционными углами.

Дирекционный угол а данного направления М₁М₂ называется прямым, а дирекционный угол а' противоположного направления ММ1 называется обратным. Как видно из рис. 20,

а = а +180⁰,

т. е. обратный дирекционный угол равен прямому плюс 180°. Эта формула является общей для всех случаев. Однако практически в тех случаях, когда а > 180° (как на рис. 21), следует применять формулу

а = а - 180⁰.

Пусть, например, а=300⁰30^/. Тогда а^/=300°30'+180°=480⁰30', или а^/=480°30-360°=120°30'. По последней формуле тот же ответ получается проще:

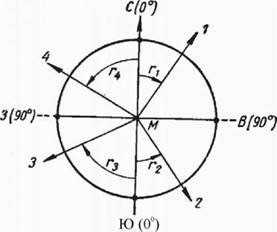Рис. 22. Четверти в которых расположены румбы а' = 300° 30' - 180° = 120° 30'.

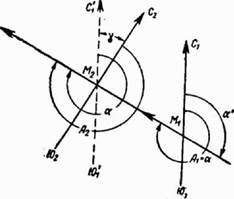
Рис. 21. Прямой и обратный дирекционные углы

Румбы. Иногда на практике удобнее определять направление линий острыми углами. В этих случаях пользуются румбами. Румбом, называется острый горизонтальный угол отсчитываемый от ближайшего направления

меридиана (северного или южного) до данной линии. Румбы могут иметь значения только в пределах между 0 и 90°. На рис. 22 обозначены румбы четырех линий М1, М2, МЗ и М4, направления которых на рис. 20 были определены азимутами. Чтобы определить румбом направление данной линии относительно меридиана, необходимо, кроме числового значения румба, указать название той четверти, в которой проходит линия. Так, линии М1, М2, МЗ и М4 имеют соответственно румбы СВ: г₁, ЮВ: г₂, ЮЗ: г₃, СЗ: г₄. В зависимости от того, отсчитываются ли румбы от магнитного или истинного меридиана, их называют магнитными или истинными.

Из сопоставления рис. 19 и 22 видно, что для линий северо-восточного направления азимут А₁ по величине равен румбу г₁. Для линий юго-восточного направления азимут и румб в сумме составляют 180°. Если линия проходит в юго-западной четверти, то ее азимут больше румба на 180°, и, наконец, для линий северо-западного направления азимут и румб составляют в сумме 360°. Эти соотношения позволяют переводить азимуты в румбы и обратно. Например, если азимут линии А =215°, то ее румб равен А-180°=215⁰-180⁰=35⁰ и имеет название ЮЗ. Если азимут линии А =100°, то ее румб равен 180°-А= 180°-100° =80° и имеет название ЮВ и т. д.

Если на рис. 19 меридиан СЮ рассматривать как осевой или как линию, параллельную осевому меридиану данной зоны, то углы А_ь Л₂, А₃ и А₄ представят дирекционные углы линий М1, М2, МЗ и М4 и должны быть обозначены соответственно а_ь а₂, а₃ и а₄. При этом условии на рис. 22 мы найдем соответствующие им румбы, которые назовем осевыми.

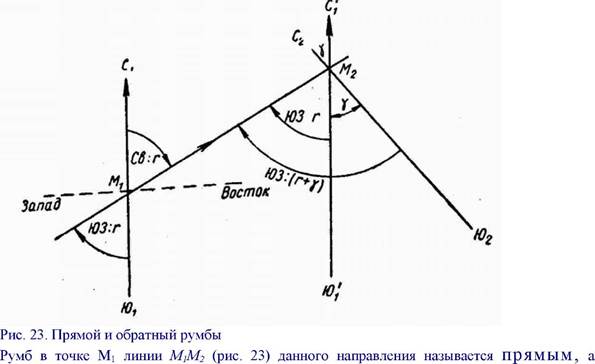
противоположного направления - обратным. Прямой и обратный румбы в одной и той же точке данной линии равны, но имеют названия противоположных четвертей. Прямой и обратный румбы одной и той же линии в разных ее точках имеют названия противоположных четвертей и отличаются на величину сближения меридианов в этих точках. Осевые прямой и обратный румбы одной и той же линии в разных ее точках имеют названия противоположных четвертей, но равны по величине. Так, например, румб СВ: г линии М]М₂ в точке М] есть прямой румб, а обратный в той же точке будет Ю3: г; обратный румб той же линии в точке М₂ будет тоже ЮЗ: г; если он осевой, и ЮЗ: (г+у) - если он истинный или магнитный.

Date: 2015-09-19; view: 1265; Нарушение авторских прав