
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Плоские прямоугольные координаты
|
|
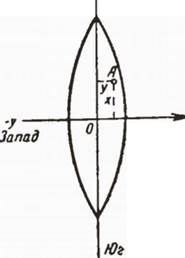
В зональной системе начало координат для всех точек данной зоны выбирается в точке пересечения среднего меридиана данной зоны с экватором (рис. 15). Изображение среднего меридиана принимается за ось абсцисс, поэтому название этого меридиана - осевой. Изображение земного экватора в виде прямой, перпендикулярной к осевому меридиану, служит осью ординат. Счет абсцисс ведется от экватора к полюсам, причем к северу от экватора абсциссы считаются положительными, к югу - отрицательными. Ординаты, отсчитываемые от осевого меридиана на восток, считаются положительными, на запад - отрицательными.
Для точки А (рис. 15) прямоугольными координатами будут: абсцисса х и ордината у. Для территории России, расположенной в северном полушарии, все абсциссы положительны. Чтобы не иметь дела с различными знаками ординат, на практике ординату точек среднего меридиана считают не за нуль, а за 500 км. Кроме того, впереди каждой ординаты указывается еще номер зоны, в которой расположена точка. Так, например, запись 7 487 230 указывает на то, что точка находится в седьмой зоне и что ее ордината
Рис. 15. Зональная система координат
У = 487 230 - 500000 = -12770 м.
Для облегчения пользования прямоугольными координатами на карту наносят сетку квадратов, образованных прямыми, параллельными осям координат и проведенными через
| *х |
| 8остов |
| к Север |
определенное число километров. Такую сетку называют километровой.
На рис. 16 показан лист карты масштаба 1:10000, ограниченный меридианами с долготами 18°00' и 18°03'45" и параллелями с широтами 54°4230 и 54°45', надписанными в углах рамки, а на самой рамке нанесены деления, обозначающие минуты дуг меридианов и параллелей. Соединяя крайние точки одноименных минутных делений северной и южной сторон рамки, а также соответствующие точки делений западной и восточной сторон, получим на карте сетку меридианов и параллелей, служащую для определения по карте географических координат ее точек и для нанесения на карту точек по географическим координатам.
Север
---------------- 9а
IV
| Р* |
| Запад |
-Восток
а, | у
I <
| III |
| II |
| Ь< |
-Ъв
Юг
Рис. 17. Произвольная система прямоугольных координат
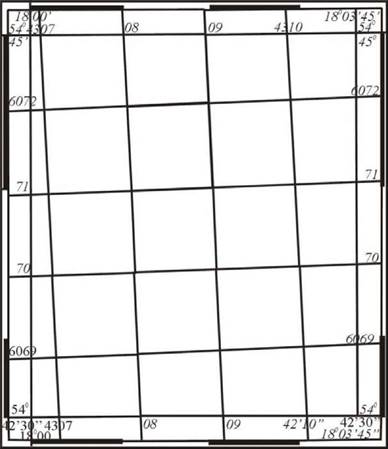 5ис. 16.Карта с нанесенной километровой сеткой
5ис. 16.Карта с нанесенной километровой сеткой
|
На том же листе карты нанесена километровая сетка линий, параллельных и перпендикулярных осевому меридиану данной зоны. Эти линии называют вертикальными и горизонтальными линиями километровой сетки. Нижняя линия сетки, перпендикулярная к осевому меридиану, имеет надпись 6 069; это означает, что все точки данной линии отстоят от экватора на 6069 км по осевому меридиану. Полная надпись таких расстояний сделана только на крайних линиях; промежуточные линии надписаны двумя последними цифрами соответствующих расстояний. Первая километровая линия, параллельная осевому меридиану, имеет надпись 4307. Здесь цифра 4 обозначает номер зоны, а три остальные цифры выражают в километрах увеличенную на 500 ординату точек этой линии, так что ее ордината равна 307 - 500= -193 км, следовательно, километровая линия расположена к западу от осевого меридиана 4-й зоны на расстоянии 193 км. Полные надписи километровых линий, параллельных осевому меридиану, также даны только для крайних линий. При помощи километровой сетки можно определять в зональной системе прямоугольные координаты точек карты и наносить на карту точки по данным их координатам. Зональная* система координат введена в практику геодезических работ с 1928 г., а в качестве общесоюзной принята в 1932 г.
Произвольная система прямоугольных координат. Часто
положение точек на плане определяют относительно системы прямоугольных координат, начало которой выбирается произвольно. В этом случае систему прямоугольных координат составляют две
взаимно перпендикулярные прямые Ох и Оу (рис. 17), называемые осями координат: Ох
называется осью абсцисс, Оу — осью ординат. Точка О пересечения осей служит началом координат. Положение любой точки А в этой системе определяется отрезками Аа=х (абсцисса) и Аа2 =у (ордината), параллельными осями координат. Значения координат х и у сопровождаются знаками плюс или минус. В геодезии принимают направление оси абсцисс совпадающим с направлением меридиана, проходящего через начало координат; за положительное направление этой оси принимают направление на север. Направление оси ординат считается положительным на восток и отрицательным на запад. Оси координат разделяют плоскость чертежа на четыре части, называемые четвертями: СВ, ЮВ, ЮЗ, СЗ; знаки координат точек, лежащих в этих четвертях, показаны в табл. 5.
Таблица 5
|
Применяемая в геодезии система прямоугольных координат называется правой, так как нумерация четвертей и направление отсчета углов в этой системе ведется по направлению движения часовой стрелки, т. е. вправо. В аналитической геометрии применяется левая система прямоугольных координат, в которой нумерация четвертей и направление отсчета углов ведется в обратном направлении, как в тригонометрии.
Легко установить, что знаки координат точек, расположенных в одноименных четвертях правой и левой систем, совпадают. Это позволяет применять формулы тригонометрии без всяких изменений независимо от того, в какой из этих систем производятся вычисления.
Date: 2015-09-19; view: 1288; Нарушение авторских прав