Сближение меридианов

При работе с картой, составленной в равноугольной поперечно-цилиндрической проекции, направления линий по карте определяют дирекционными углами. Для перехода от дирекционных углов к истинным азимутам по формулам, данным в § 16, надо знать сближение меридианов.

Приближенно сближение меридианов можно найти так. Примем общую фигуру Земли за шар, радиус которого К=6371 км (рис. 25). На какой-нибудь параллели с широтой ф возьмем две точки А и В, линейное расстояние между которыми пусть будет 1 км.

В точках А и В вообразим касательные к меридианам, проходящим через эти точки. Эти касательные называются полуденными линиями. Тогда угол между касательными представит сближение меридианов точек А и В. Для точек А и В, расположенных в пределах одной какой-нибудь зоны, угол у настолько мал, что рис. 25 расстояние I можно рассматривать как дугу радиуса АТ. Тогда угол у, выраженный в радианах, будет

I

7 =-----,

АТ

Но

К

АТ = К1§(90⁰ -ф) = Ка§ф = ■

*8Ф

следовательно,

I

7 = — К

Так как в одном радиане 3438', то сближение меридианов, выраженное в минутах, будет

равно

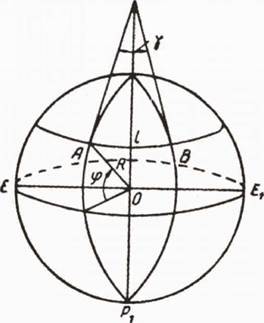Рис. 25.Сближение меридианов

' I '

у =— 1дт. 3438.

К

Подставив сюда вместо К его значение, получим

у'= 0,540/^ •

Если 1_кт=1, то

у = 0,540^.

т. е. приближенно сближение меридианов на один километр (выраженное в минутах) равно половине тангенса широты места. Так, для точки с ф=55°46' по формуле (1У.5') у=0',8.

При определении направлений во многих случаях ошибка в 1' считается допустимой. В таких случаях сближением меридианов на 1 км можно пренебречь, и на этом расстоянии меридианы в соответствующих точках можно рассматривать как параллельные.

(ТУ.5')

Глава V. РЕЛЬЕФ МЕСТНОСТИ И ЕГО ИЗОБРАЖЕНИЕ

$ 20. Методы изображения рельефа на планах и картах

Для изображения рельефа на планах и картах в тех случаях, когда важнее всего точность изображения, применяется метод горизонталей.

Горизонтали. Горизонталь на местности можно представить как след, образованный пересечением поверхности воды с физической поверхностью Земли на изображаемом участке. Лучшим примером горизонтали на местности служит береговая линия стоячей воды.

Представим себе, что какой-нибудь холм весь залит водой и уровень воды имеет отметку 100 м относительно некоторого условного горизонта. Предположим теперь, что уровень воды упал на 5 м и часть холма обнажилась. Отметка нового уровня воды теперь 95 м. След, образованный пересечением этого уровня с поверхностью холма, и представляет 95-ю горизонталь на местности. Очевидно, это замкнутая кривая.

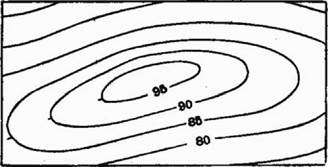
Рис. 26. Изображение местности горизонталями

Уменьшенное изображение горизонтальной проекции этой кривой представит соответствующую горизонталь на плане. Предположим, что уровень воды еще упал на 5 м, тогда получим представление о следующей, 90-й горизонтали и т. д. В результате будем иметь на плане ряд замкнутых горизонталей (рис. 26),. по виду и расположению которых можно судить о виде холма.

Разность высот двух последовательных горизонталей называется высотой сечения. В зависимости от масштаба, характера рельефа я назначения плана (карты) высоты сечения принимают равными 1, 2, 5, 10 м и т. д.

Date: 2015-09-19; view: 1206; Нарушение авторских прав