
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Влияние кривизны Земли на горизонтальные и вертикальные расстояния
|
|
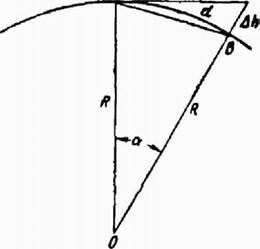
Примем общую фигуру Земли за сферу радиуса К. (рис. 9) и выберем на ней две произвольные точки А и В. Расстояние между этими точками пусть будет й, а центральный угол, соответствующий дуге й, обозначим а. Вместо сферической поверхности возьмем плоскость, касательную к ней в точке А, и продолжим радиус ОВ до пересечения с этой плоскостью в точке С. Пусть при этом отрезок касательной АС=г, тогда в горизонтальном расстоянии между точками А и В произойдет ошибка Ай=г-а, а в вертикальном АЬ=ОС—ОВ, из рис.9 находим 1=К1§а и й=Ка, где угол
а
а = — (111.1)
К
выражен в радианах.
Тогда Ай=К(1§ а - а). Так как практически, а весьма незначительно в сравнении с К, то угол а настолько мал, что приближенно можно принять
а3
гда - а = —. 3
Учитывая (111.1), найдем
Я! С
|
Рис. 9 Определение расстояния с учетом кривизны Земли.
а=1 й!
3 = 3 К2
Приняв К=6371 км: й=10 км, по формуле (Ш.2) получим ЛЬ= 1 см и ЛЬ: й =1: 1000000. Отсюда следует, что заменяя дугу АВ отрезком касательной АС, при расстояниях до 10 км сделаем ошибку, меньшую 1: 1 000000 длины этой дуги. Такая ошибка считается допустимой при самых точных измерениях горизонтальных расстояний на земной поверхности. С увеличением же й ошибка Лй растет очень быстро, так как она пропорциональна кубу расстояний.
Угол ВАС = 1а как угол, составленный касательной и хордовой. По малости этого угла 2
отрезок ЛЬ можно рассматривать как дугу радиуса й. Тогда
АИ = —а • й. 2
Подставив вместо а его выражение из формулы (111.1) найдем
л, 1 й3
АИ = -• —. (1113)
2К
Придавая в формуле (III.3) различные числовые значения й, получим значения ЛЬ, приведенные в табл.1. Таблица 1
| й (км) | 0.5 | |||
| АИ (см) |
Для инженерных целей высоты точек земной поверхности необходимо бывает определять с относительно высокой точностью, допуская на 1 км ошибку не более 2 см. Отсюда заключаем, что
при измерении вертикальных расстояний нельзя пренебрегать кривизной Земли даже при небольших горизонтальных расстояниях между точками.
| Ай = К— = - — (111.2) |
Обращаясь снова к рис.2, заметим, что в горизонтальной плоскости МЫ в пределах площади круга диаметром 20 км отрезки аЪ, Ъс, ей... практически сохраняют ту же длину, что и на сфере. Углы между этими отрезками от замены сферической поверхности плоскостью МЫ также практически не изменят своей величины. Поэтому и вся фигура аЪсйе как да сфере, так и на плоскости практически будет изображаться одинаково. В этом смысле мы и говорим, что контуры местности при проектировании их на плоскость в пределах площади круга диаметром 20 км изобразятся без искажений, вызываемых кривизной Земли.
$ 12. Понятие о карте. Различие между картой и планом
В тех случаях, когда на плоскости изображают значительную территорию, нельзя пренебрегать кривизной Земли, а следует ее учитывать. На больших площадях проектирование контуров отвесными линиями производят уже не на плоскость, а на сферическую поверхность; при этом отвесные линии в различных точках земной поверхности нужно считать не параллельными между собой, а пересекающимися в центре сферы.
Сферическая поверхность не может быть развернута на плоскости без складок и разрывов, поэтому спроектированные на сферическую поверхность контуры местности не могут быть перенесены на плоскость бумаги с сохранением подобия, т. е. без искажений. Задача при этом состоит не в полном устранении искажений, что невозможно, а в уменьшении искажений и в математическом определении их значений с тем, чтобы по искаженным изображениям можно было с
помощью вычислений получать действительные величины. Построенные по определенным математическим законам уменьшенные изображения на плоскости значительных частей земной поверхности, размеры которых не позволяют пренебрегать кривизной Земли, называются картами.
При создании карт прежде всего строят географическую сеть меридианов и параллелей, называемую картографической сеткой, внутри которой располагают изображаемые контуры.
Картографическая сетка служит внешним признаком, отличающим карту от плана. Существенное же различие между картой и планом состоит в следующем:
1. план - это изображение проекций небольших участков земной поверхности на горизонтальную плоскость; карта - изображение проекций больших территорий Земли на сферическую поверхность;
2. длины, углы и площади контуров горизонтальной проекции на плане не искажаются, а
на картах, вообще говоря, искажаются.
Другими словами, масштаб плана остается постоянным для всех частей плана. На картах же и в особенности на тех, которые изображают всю Землю или большую часть ее поверхности, масштаб меняется не только в различных частях карты, но и по различным направлениям, выходящим из одной точки.
При построении карты предполагают, что поверхность Земли изображается сначала на глобусе определенного размера, а затем уже с его поверхности переносится на плоскость.
Вдоль одной или нескольких линий (меридианов, параллелей или других линий) масштаб картографической сетки равен масштабу глобуса, служащего основанием для построения карты. Этот масштаб называется главным. В других частях сетки масштабы будут иные. Их называют частными.
Чем меньше часть земной поверхности, которую охватывает карта, тем ближе карта по своим свойствам к плану и тем меньше уклонения частных масштабов от главного. Значительные уклонения частных масштабов от главного имеют географические карты, которые охватывают большие территории; они дают обобщенную характеристику местности и составлены в очень мелких масштабах. Топографические карты, служащие для подробного ознакомления с местностью, составляемые в более крупных масштабах и охватывающие на отдельных листах сравнительно небольшие территории, по своим свойствам весьма близки к планам.
Влияние масштаба на содержание и использование карт так велико, что карты принято классифицировать по масштабам, различая карты крупного, среднего и мелкого масштабов. Такое деление условно. В советской практике принято считать крупномасштабными карты масштабов 1:100000 и крупнее, среднемасштабными — от 1:200000 до 1:1000000 и мелкомасштабными— мельче 1:1000000.
Крупномасштабные карты называются топографическими. Это наиболее подробные карты с изображением на них контуров и рельефа земной поверхности.
Основной государственной картой России является карта масштаба 1:1 000000. Размер рамки каждого листа этой карты составляет 4° по широте и 6° по долготе. В северных широтах от 60 до 76° листы сдваиваются, а от 76 до 88° учетверяются по долготе. Размерам рамки листа миллионной карты, на котором находится Москва, соответствует на местности площадь приблизительно в (444 х 372) км2.
Каждому
листу картыРис. 20 Система обозначения листов карты М 1:1000000
миллионного
масштаба соответствуют 144 листа масштаба 1:100000; московскому листу карты этого масштаба на местности соответствует площадь приблизительно в (37 х 31) км2. Каждый лист карты масштаба 1:100000 охватывает территорию, при изображении которой кривизна Земли практически почти неощутима. Тем более это справедливо для листов карт более крупных масштабов.
Листу карты масштаба 1:100000 соответствуют 4 листа карты масштаба 1:50000. Размеры рамки московского листа карты пятидесятитысячного масштаба примерно соответствуют площади в
| ( |
37 1 ч 2 2
— х—) км, или (18,5х15,5) км. Следовательно, каждым листом карты масштаба 1:50 000 и 2 2
крупнее можно пользоваться как планом.
Номенклатура карт и планов
|
Для удобства пользования многолистной картой каждый ее лист получает определенное обозначение, причем расположение отдельных листов указывается в особой таблице, называемой сборно й. Система обозначения отдельных листов карты называется номенклатурой карты.
В основу номенклатуры карт различных масштабов в России положена государственная карта масштаба 1:1000000.
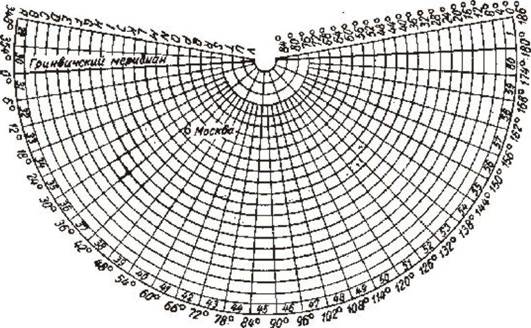
Деление на листы этой карты выполняется следующим образом. Вся земная поверхность делится меридианами, проводимыми через 6°, на 60 колонн. Колонны нумеруются арабскими цифрами; счет колонн ведется с запада на восток от меридиана с долготой 180° (рис. 10). Колонны в свою очередь разделяются на ряды параллелями, проводимыми через 4°. Ряды обозначаются заглавными буквами латинского алфавита, счет рядов ведется от экватора к северному и южному полюсам. Проведенные таким образом меридианы и параллели служат рамками отдельных листов карты.
Номенклатура листа складывается из указания ряда и колонны, в которых расположен данный лист; например, N-37—номенклатура листа, на котором находится Москва.
| А | Б |
| В | Г |
| 6 |
|
1:200000
| 42 36 56' |
| 42, |
| I I |
| Т | Т | 3 | Т | Г | т | г | г | 71 | гт | У | |
| а | |||||||||||
| !Е | |||||||||||
| В | |||||||||||
| I | |||||||||||
| в | |||||||||||
| 5? | |||||||||||
| 10! | |||||||||||
| □3 | а | ы< | у | .1 |
1:100000
1:500000
Рис. 11 Номенклатура листов карт среднего масштаба
Одному листу карты масштаба 1:1000000 соответствуют: 4 листа карты масштаба 1:500000, обозначаемые заглавными буквами русского алфавита А, Б, В, Г, присоединяемыми к номенклатуре миллионного листа; 9 листов карты масштаба 1:300000,
обозначаемые римскими цифрами I—IX, помещаемыми впереди номенклатуры миллионного листа; 36 листов карты масштаба 1:200 000, обозначаемые римскими цифрами I—XXXVI, присоединяемыми справа к номенклатуре миллионного листа; 144 листа карты масштаба 1:100000, обозначаемые арабскими цифрами 1—144, следующими за номенклатурой миллионного листа (рис. 11). Данные этой разграфки для листа карты N-37 масштаба 1:1 000000 приведены в табл. 2. Таблица 2
| Масштаб | Число листов в | Номенклатура | Размер рамки | |
| карты | одном листе карты масштаба 1:1000000 | последнего листа | ||
| По широте | По долготе | |||
| 1:500000 | N-37^ | 20 | 30 | |
| 1:300000 | ^-N-37 | 1020' | 20 | |
| 1:200000 | N-37-XXXVI | 10 | ||
| 1:100000 | N-37-144 |
N-37-144
| 52 20' |
| 52°10' |
| 52°10' |
| о л' |
| 52°0' |
| 52 О |
41°30" 41°45'
42°о:
52 20'
| А | Б |
| в | Г |
1:50000
Рис. 12. Номенклатура листа карты М 1:50000
| 52 10 |
| 0г " |
| 52°5' |
| 52 5 |
| 52°0* |
| 52°0' |
N-37-144-Г
о 4}ЧУ 41°52'30'~ 42°о;„0
52 10"
| __ г 1 | 1--- | б |
| В | Г |
1:250000 и 1:10000
Рис. 13. Номенклатура листов карт М 1:25000 и М 1:10000
Лист карты масштаба 1:100000 служит основой для разграфки и номенклатуры листов карт более крупных масштабов. Одному листу карты масштаба 1:100000 соответствуют 4 листа карты масштаба 1:50000, которые обозначаются заглавными буквами русского алфа вита А, Б, В, Г, присоединяемыми к номенклатуре стотысячного листам Каждый такой лист (рис. 12) имеет рамку размером 10' по широте и 15—по долготе. Номенклатура последнего листа, соответствующего листу карты N-37-144 масштаба 1:100000, будет N-37-144-1'. Одному листу масштаба 1:50 000 соответствуют 4 листа масштаба 1:25 000, которые обозначаются строчными буквами русского алфавита а, б, в, г, присоединяемыми к номенклатуре пятидесятитысячного листа (рис. 13); одному листу масштаба 1:25000 соответствуют 4 листа масштаба 1:10000, обозначаемые арабскими цифрами 1—4, следующими за номенклатурой двадцатипятитысячного листа.
Данные для разграфки листа карты масштаба 1:100000 на листы карт более крупных масштабов представлены в табл. 3.
Таблица 3
|
Лист карты масштаба 1:100000 служит также основой для разграфки и номенклатуры листов планов масштабов 1:5000 и 1:2000.
Одному листу карты масштаба 1:100000 соответствуют 256 (16 х 16) листов плана масштаба 1:5000, которые обозначаются цифрами 1, 2,..., 256, заключаемыми в скобки. Каждый такой лист
20',,, 30',,,
имеет рамку размером = 115 по широте и ^^ = 152,5 по долготе. Номенклатура последнего
листа плана масштаба 1:5000, соответствующего листу карты N-37-144 масштаба 1: 100000, будет N 37-144-(256).
Одному листу плана масштаба 1:5000 соответствуют девять листов плана масштаба 1:2000, которые обозначаются строчными буквами русского алфавита а, б, в, г, д, е, ж, з, и, заключаемыми в
115'',, 1'52",5 г
скобки. Каждый такой лист имеет рамку размером —3— = 25 по широте и —3— = 37,5 по
долготе. Номенклатура последнего листа плана масштаба 1:2000, соответствующего листу N-37-144- (256), будет ^37-144-(256-и). Приведенные данные представлены в табл. 4.
$ 14. Равноугольная поперечно-цилиндрическая проекция
Положение точек земной поверхности на глобусе определяется географическими координатами при помощи градусной сетки, а на карте - теми же координатами при помощи картографической сетки. На плане и топографической карте для той же цели пользуются плоскими прямоугольными координатами. Чтобы установить связь между географическими координатами любой точки Земли на сфере или сфероиде и прямоугольными координатами той же точки на плоскости, применяют особый способ проектирования всего земного шара на плоскость по частям, или по так называемым зонам; весь земной шар разделяют при этом меридианами на шести- или трехградусные зоны, простирающиеся от северного полюса к южному (рис. 14).
Таблица 4
|
Деление поверхности земного шара на шестиградусные зоны соответствует разграфке листов миллионной карты. Счет зон ведется на восток от нулевого меридиана, проходящего через Гринвич, а счет колонн - на восток от меридиана с долготой 180°, поэтому номер зоны для данного листа миллионной карты равен номеру колонны минус 30. Так, для листа миллионной карты, имеющего номенклатуру N-37, зона будет иметь номер 7. Отсюда легко сообразить долготы меридианов на восточной и западной границах этой зоны. Долгота восточного меридиана, очевидно, будет 6° х 7=42°, а западного 42°- 6°=36°. Средний меридиан седьмой зоны имеет долготу 39°. Каждую данную зону проектируют на плоскость отдельно при помощи цилиндра.
Если общую фигуру Земли рассматривать как сферу, то цилиндр должен иметь в поперечном сечении круг. Ось такого цилиндра, проходящую через центр сферы, надо вообразить в плоскости земного экватора так, чтобы шар касался цилиндра по среднему меридиану г данной зоны. На поверхность такого цилиндра и проектируют избранную зону под условием сохранения равенства углов на сфере и на цилиндре, а затем цилиндр развертывают на плоскости. В результате получают изображение данной зоны в проекции на плоскость (рис.15). Такая проекция называется равноугольной поперечно - цилиндрической*. так как она получается при помощи цилиндра, ось которого расположена поперек земной оси, и углы местности изображаются в этой проекции без искажений. Средний меридиан зоны изображается прямой. Вся зона переходит со сферы на плоскость в несколько расширенном виде.
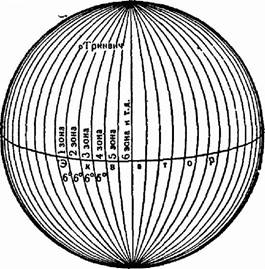 Рис. 14.Разбивка фигуры Земли на 6-ти градусные зоны.
Рис. 14.Разбивка фигуры Земли на 6-ти градусные зоны.
|
Все длины линий в этой проекции несколько преувеличены по сравнению с их натуральными горизонтальными проекциями; искажения длин тем больше, чем дальше линия расположена от среднего меридиана зоны. На границах зон в пределах широт от 30 до 70° относительные ошибки, происходящие от искажения длин линий в этой проекции, колеблются от 1:1000 до 1:6000. Когда такие ошибки недопустимы, прибегают к трехградусным зонам.
На картах, составленных в равноугольной поперечно-цилиндрической проекции, искажения длин в различных точках проекции различны, но по разным направлениям, выходящим из одной и той же точки, эти искажения будут одинаковы. Круг весьма малого радиуса, взятый на уроненной поверхности, изобразится в этой проекции тоже кругом. Поэтому говорят, что рассматриваемая проекция конформна, т. е. сохраняет подобие фигур на сфере и в проекции при весьма малых размерах этих фигур. Таким образом, изображения контуров земной поверхности в этой проекции весьма близки к тем, которые получаются на планах, а вблизи среднего меридиана зоны практически такие же, как и на планах.
Проектируя последовательно одну зону за другой, можно представить в этой проекции всю поверхность земного шара. В географическом отношении такая проекция не имеет практического значения, так как она дает не сплошное изображение всей земной поверхности, а с разрывами, увеличивающимися к полюсам. Эта проекция ценна тем, что она, во-первых, позволяет выбирать системы плоских прямоугольных координат по всей поверхности Земли с единым началом координат для каждой данной зоны; во-вторых, дает возможность находить по географическим координатам любой точки земного шара или сфероида прямоугольные координаты ее изображения и, наоборот, по данным плоским прямоугольным координатам точки в этой проекции вычислить соответствующие им географические координаты на сфере или на сфероиде.
Date: 2015-09-19; view: 2681; Нарушение авторских прав