
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Современная стоимость постоянной ренты постнумерандо
|
|
Годовая рента. Напомним, что под современной стоимостью потока платежей понимают сумму дисконтированных членов этого потока на некоторый предшествующий момент времени. Вместо термина "современная стоимость" (современная величина) потока платежей в зависимости от контекста употребляют термины капитализированная стоимость или приведенная ее-личина. Как было показано выше, современная стоимость потока платежей эквивалентна в финансовом смысле всем платежам, которые охватывает поток. В связи с этим данный показатель находит широкое применение в разнообразных финансовых расчетах (планирование погашения долгосрочных займов, реструктурирование долга, оценка и сравнение эффективности производственных инвестиций и т.д.). В общем виде метод определения современной величины потока платежей (метод прямого счета) рассмотрен в § 5.1. Здесь же объектом анализа является постоянная финансовая рента постнумерандо.
Методы расчета современных стоимостей финансовых рент обсудим в том же порядке, что и методы наращения рент и почти столь же детально. Начнем с самого простого случая — годовой ренты постнумерандо, член которой равен R, срок ренты — п, ежегодное дисконтирование. Рента немедленная. В этих условиях дисконтированная величина первого платежа равна Rv, второго — Rv2, последнего — Rv". Как видим, эти величины образуют ряд, соответствующий геометрической профессии с первым членом Rv и знаменателем v. Обозначим сумму членов этой профессии через А:
A-Ryv' = Rv- ----------- --R—V--
h v-i
/ х- (5-14)
1- (l + i)
I
Назовем множитель, на который умножается R, коэффициентом приведения ренты, он обозначен как апЧ (в литературе встречается обозначение an,j). Этот коэффициент характеризует современную стоимость ренты с членом, равным 1. Значения an;i табулированы (см. табл. 7 Приложения).
Поскольку рассматриваемый параметр часто применяется в финансовых расчетах, полезно, обратить внимание на некоторые его свойства. Очевидно, что чем выше значение /', тем меньше величина коэффициента. Нетрудно показать, что при / = О
%=о = Л-
При увеличении срока ренты величина апЛ стремится к некоторому пределу. При п =» предельное значение коэффициента составит
Lim
!-(!♦«)-
(5.15)
Полученное выражение применяется при расчете современной стоимости вечной ренты, о чем пойдет речь в § 5.5.
График зависимости апЧ от п показан на рис. 5.2.
Воспользуемся формулой (5.14) для определения взаимосвязи коэффициентов приведения ограниченной и вечной рент:
"„;/ =
(1 + /Г" 1 1
. =7 " ° + °~" х у = ° " уМ)а~*т
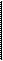 В последней записи искомый коэффициент приведения определен как доля коэффициента приведения вечной ренты, зависящая от срока ренты.
В последней записи искомый коэффициент приведения определен как доля коэффициента приведения вечной ренты, зависящая от срока ренты.
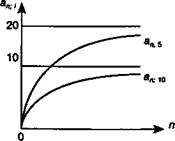
Рис. 5.2
ПРИМЕР 5.9. Годовая рента постнумерандо характеризуется параметрами: Я = 4 млн руб, п = 5. При дисконтировании по сложной ставке процента, равной 18,5 % годовых, получим
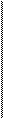
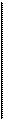 1 - 1.185"5
1 - 1.185"5
А = 4a*iRs = 4 х-------- ГТ^------ = 4 х 3,092 = 12,368 млн руб.
О,185
Таким образом, все будущие платежи оцениваются в настоящий момент в сумме 12,368 млн руб. Иначе говоря, 12,368 млн руб., размещенных под 18,5% годовых, обеспечивают ежегодную выплату по 4 млн руб. в течение 5 лет.
Заметим, что формула (5.14) может быть применена и для определения современной стоимости /ьсрочной ренты. В этом случае переменная п означает число периодов ренты, а / — ставку за один период (но не годовую).
Коэффициент приведения ренты за срок п = л, + п2 определяется следующим образом:
ан;1 - Я*,;/
+ в|.2У1- (5.16)

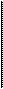 Годовая рента, начисление процентов т раз в году. Не будем выводить формулу для этого случая, а просто заменим в формуле (5.14) дисконтный множитель (1 + /)~/| на эквивалентную величину (1 + j/m)~mn, соответственно, / заменим на (1 + j/m)m -— 1, после чего имеем:
Годовая рента, начисление процентов т раз в году. Не будем выводить формулу для этого случая, а просто заменим в формуле (5.14) дисконтный множитель (1 + /)~/| на эквивалентную величину (1 + j/m)~mn, соответственно, / заменим на (1 + j/m)m -— 1, после чего имеем:
1 -(1 +7/тГ'™
Л = R /л ,.. чт------ — = Ramn.i/m. (5.17)
(1 +у//и)т - 1 mnj/m
Рента /^-срочная (т = 1). Если платежи производятся не один, а р раз в году, то коэффициенты приведения находятся так же, как это было сделано для годовой ренты. Только теперь размер платежа равен R/p, а число членов составит пр. Сумма дисконтированных платежей в этом случае равна
А - -? vt/p - R r1"'1+l'---------- - Ra{p). (5.18)
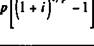
ПРИМЕР 5.10. В первой главе упоминалась авария на химическом заводе в Бхопале (Индия). Корпорация "Юнион Карбайд" предложила в качестве компенсации пострадавшим 200 млн долл., выплачиваемых в течение 35 лет. Предложение было отклонено ("За рубежом". 1985. № 11). Предложенная компенсация
 эквивалентна 57,5 млн долл., выплаченных единовременно. Покажем, как была рассчитана эта сумма.
эквивалентна 57,5 млн долл., выплаченных единовременно. Покажем, как была рассчитана эта сумма.
Если выплаты производятся помесячно на протяжении 35 лет равными суммами, то данный ряд платежей представляет собой постоянную ренту (р = 12) с годовой суммой выплат 200/35 = = 5,714 млн долл. в год. Допустим, это рента постнумерандо. Тогда согласно (5.18), положив / = 10%, получим
1 - 1,1-35 А = 5,714 1 11/12 _ = 57,59 млн долл.
Иначе говоря, капитал в сумме всего 57,59 млн долл. при начислении 10% годовых достаточен для выполнения обязательства.
Рента ^-срочная (р = /и). Число членов ренты здесь равно числу начислений процентов; величина члена ренты составляет R/m. В итоге
R 1 -(1 +7/w)-"w1 -(1 +у/тГ™
А = х------------------ = R ----------:--------. (5.19)
т j/m j
Этот же результат можно получить и по формуле (5.14) и при этом воспользоваться таблицей коэффициентов приведения постоянных рент. В этом случае вместо числа лет берется количество периодов ренты, процентная ставка и величина члена ренты определяются соответствующим образом.
Для расчета современной стоимости платежей ренты с условием р = т можно воспользоваться программой ПЗ (PV) пакета Excel, которая определяет величину А с учетом единовременного взноса в конце срока. Расчет производится по формуле
А = R х an;i + БС х (1 + /ГЛ,
где R — член ренты, БС — единовременный взнос, an;i — коэффициент приведения постоянной ренты, п — число'периодов выплаты ренты и начисления процентов, / — процентная ставка за период.
Date: 2015-09-19; view: 728; Нарушение авторских прав