
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Формулы для расчета срока постоянных рен
|
|
| Количество | Количество начислений | Исходны | ||||
| платежей | S | |||||
| от = 1 от > 1 | 1пф+П | (5.28) | ||||
| /> = i | " ~ 1п(1 + /) | |||||
| ln{jl(l+j/mr-l) + l} | (5.30) | |||||
| от1п(1 + у/от) | ||||||
| от= 1 т= р т * р | 1п{^[(1 + О'/" - 1] + 1} | (5.32) | ||||
| Р>\ | 1п(1 + /) | |||||
| 1пф+1) | (5.34) | |||||
| /nln(l +у/от) | ||||||
| ln{^p[(l+y/m)^-l] + l} | • (5.36) | |||||
| /nln(l + j/m) |
1.  Расчетные значения срока будут, как правило, дробные. В этих случаях для годовой ренты в качестве п часто удобно принять ближайшее целое число лет. У /ьсрочной ренты результат округляется до ближайшего целого число периодов пр. Например, пусть для квартальной ренты получено п = 6,28 лет, откуда пр = 25,12 кварталов. Округляем до 25, в этом случае п = 6,25 лет.
Расчетные значения срока будут, как правило, дробные. В этих случаях для годовой ренты в качестве п часто удобно принять ближайшее целое число лет. У /ьсрочной ренты результат округляется до ближайшего целого число периодов пр. Например, пусть для квартальной ренты получено п = 6,28 лет, откуда пр = 25,12 кварталов. Округляем до 25, в этом случае п = 6,25 лет.
2. Если округление расчетного срока производится до меньшего целого числа, то наращенная сумма или современная стоимость ренты с таким сроком оказывается меньше заданных размеров. Возникает необходимость в соответствующей компенсации. Например, если речь идет о погашении задолженности путем выплаты постоянной ренты, то компенсация может быть осуществлена соответствующим платежом в начале или конце срока, или с помощью повышения суммы члена ренты.
Обсудим еще одну проблему, связанную со сроком ренты. Пусть А — текущее значение долга. Если он погашается с помощью постоянной ренты, то из (5.14) следует, что долг может быть погашен за конечное число лет только при условии, что R > AL Аналогичные неравенства можно найти и для других видов рент. Если условия ренты таковы, что имеет место равенство, например, R = Ai9 то п = оо9 т.е. рента окажется вечной и долг практически не может быть погашен.
ПРИМЕР 5.15. Какой необходим срок для накопления 100 млн руб. при условии, что ежемесячно вносится по 1 млн руб, а на накопления начисляются проценты по ставке 25% годовых? Имеем Я = 12, / = 25%. По формуле (5.32) находим
In п = —
-^-12(1,251/i2- 1) + 1
П1,25
= 4,7356 года.
Если срок округляется до 5 лет, то необходимо несколько уменьшить размер члена ренты, т.е. найти член ренты для п = 5. В этом случае ежемесячный взнос должен составить 914,79 тыс. руб. (см. (5.26)).
Определение размера процентной ставки. Необходимость в определении величины процентной ставки возникает всякий раз, когда речь идет о выяснении эффективности (доходности) соответствующей финансово-банковской или коммерческой операции. Заметим, что расчет процентной ставки по осталь-
ным параметрам ренты не так прост, как это может показаться на первый взгляд. В простейшем случае задача ставится следующим образом: решить уравнения (5.4) или (5.14) относительно /. Нетрудно убедиться в том, что алгебраического решения нет. Для получения искомой величины раньше прибегали к линейной интерполяции или какому-либо итерационному методу. В современных условиях для определения ставки по заданным параметрам постоянной ренты удобно воспользоваться пакетом Excel — программа НОРМА (Rate). Однако эта программа не позволяет определить ставку для переменных и непрерывных рент, в связи с чем для решения задачи следует прибегнуть к методу Ньютона—Рафсона или методу секущей (см. Математическое приложение к гл. 6). Что касается общего потока платежей, то в пакете Excel имеется программа расчета ставки для произвольного потока с равными интервалами между платежами постнумерандо. Эту программу мы применим в гл. 12 при расчете внутренней нормы доходности ВНДОХ (IRR).
В методических целях, вероятно, целесообразно начать с линейной интерполяции. По заданным R и 5, или R и А, находят значения коэффициентов наращения или приведения ренты:
sn;i=S/R; апи = А/Я.
Для оценки / применяется следующая интерполяционная формула:
/=//+ ^Vjifr-fr (5.38)
где ad и ai — табличные значения коэффициентов наращения или приведения рент для верхнего и нижнего уровня ставок (/^ /,), а — значение коэффициента наращения или приведения, для которого определяется размер ставки.
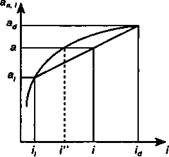
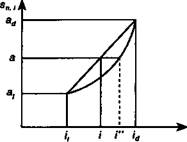
На рис. 5.3 и 5.4 изображены зависимости соответствующих коэффициентов от размера процентной ставки, а также интерполяционные оценки и точные ее значения. Первые обозначены как /, вторые как /".
Как видно из рисунков, оценки размера процентной ставки несколько отличаются от точных значений этой величины, причем, если за основу взят коэффициент приведения, то оценка оказывается завышенной. В свою очередь оценка / по коэффи-
|
|
Рис. 5.3
Рис. 5.4
 циенту наращения меньше точного значения. Чем меньше диапазон /;+ /^ тем точнее оценка процентной ставки.
циенту наращения меньше точного значения. Чем меньше диапазон /;+ /^ тем точнее оценка процентной ставки.
Применим теперь для расчета ставки программу НОРМА (Rate) пакета Excel.
Date: 2015-09-19; view: 774; Нарушение авторских прав