Теорема о движении центра масс

В ряде случаев для определения характера движения системы (особенно твёрдого тела) достаточно знать закон движения её центра масс. Чтобы найти этот закон, обратимся к уравнениям движения системы.

Рассмотрим систему, состоящую из материальных точек. Выделим какую-нибудь точку системы с массой т_k. Обозначим равнодействующую всех приложенных к точке внешних сил (активных и реакции связей) через ,а равнодействующую всех внутренних сил – через 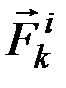. Если точка имеет при этом ускорение 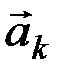,то, по основному закону динамики,

.

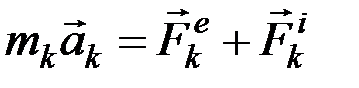Аналогичный результат получим для любой точки. Следовательно, для всей системы будет:

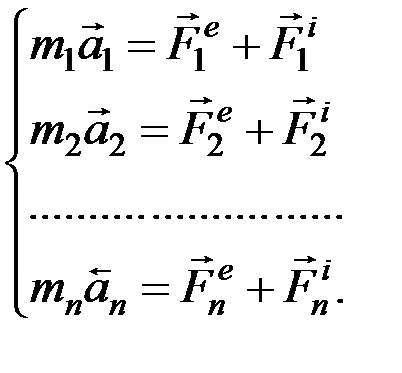(7.1)

Уравнения, используя которые, можно определить закон движения каждой точки системы, называются дифференциальными уравнениями движения системы в векторной форме.

Обобщив уравнения (7.1), получим

. (7.2)

Преобразуем левую часть равенства. Из формулы (5.4) для радиус-вектора центра масс получим:

.

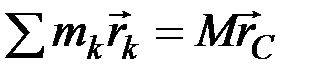Взяв от обеих частей этого равенства вторую производную по времени и заметив, что производная от суммы равна сумме производных, найдём:

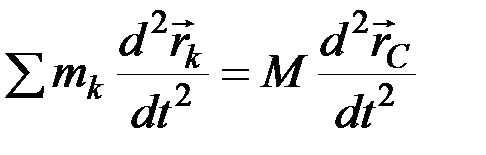
или

, (7.3)

где 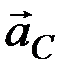– ускорение центра масс системы. Так как по свойству внутренних сил системы (см. раздел 5.1) 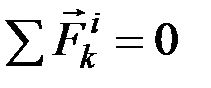, то, подставив все найденные значения в равенство (7.2), получим окончательно:

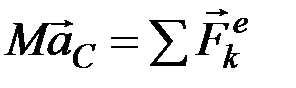. (7.4)

Уравнение (7.4) выражает теорему о движении центра масс системы. По внешнему виду оно совпадает с уравнением, определяющим закон движения материальной точки, у которой масса 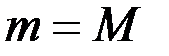, а действующие силы равны 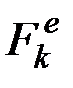. Следовательно, доказанная нами теорема о движении центра масс может быть сформулирована следующим образом: центр масс системы движется как материальная точка, масса которой равна массе всей системы и к которой приложены все внешние силы, действующие на систему.

Проектируя обе части равенства (7.4) на оси координат, получим:

,

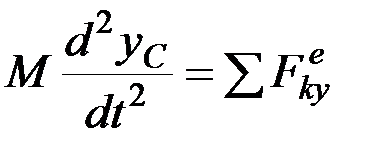, (7.5)

.

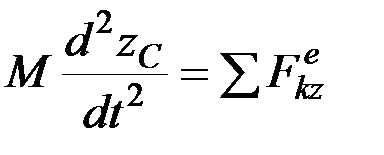Эти уравнения представляют собой дифференциальные уравнения движения центра масс в проекциях на декартовы оси координат.

Контрольные вопросы

1. Что называют моментом инерции твёрдого тела относительно плоскости, оси и точки?

2. Какую величину называют радиусом инерции тела относительно оси?

3. При каких условиях некоторая ось является главной осью инерции твёрдого тела?

4. Что называется центробежным моментом инерции твёрдого тела?

5. Какими свойствами обладают главные оси инерции?

6. Как вычисляют момент инерции твёрдого тела относительно произвольной оси, проходящей или не проходящей через центр масс тела?

7. Как в динамике классифицируют силы, действующие на точки механической системы?

8. Что называют центром масс системы точек, как определяют его координаты?

9. Дайте формулировку теоремы о движении центра масс.

Date: 2015-09-03; view: 467; Нарушение авторских прав