
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Центробежные моменты инерции. Главные оси инерции тела
|
|
Момент инерции тела относительно оси не характеризует распределение масс системы полностью. Поэтому в механике в качестве характеристик, учитывающих асимметрию в распределении масс, вводят ещё так называемые центробежные моменты инерции. Если через точку  провести координатные оси
провести координатные оси 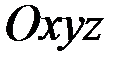 ,то по отношению к этим осям центробежными моментами инерции (или произведениями инерции) называют величины
,то по отношению к этим осям центробежными моментами инерции (или произведениями инерции) называют величины  ,
,  ,
,  определяемые равенствами:
определяемые равенствами:
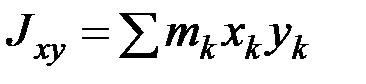 ,
,
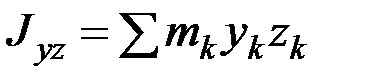 , (6.16)
, (6.16)
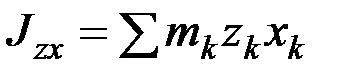 ,
,
где  – массы точек,
– массы точек, 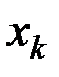 ,
, 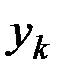 ,
, 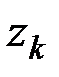 – их координаты, при этом
– их координаты, при этом  и т.д.
и т.д.
Для сплошных тел формулы (6.16) принимают вид:
 . (6.17)
. (6.17)
В отличие от осевых, центробежные моменты инерции могут быть как положительными, так и отрицательными величинами и, в частности, при определённым образом выбранных осях 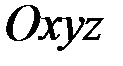 могут обращаться в нули.
могут обращаться в нули.
Рассмотрим однородное тело, имеющее ось симметрии. Проведём координатные оси 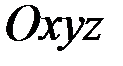 так, чтобы ось
так, чтобы ось 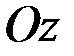 была направлена вдоль оси симметрии. Тогда в силу симметрии каждой точке тела с массой
была направлена вдоль оси симметрии. Тогда в силу симметрии каждой точке тела с массой  и координатами
и координатами 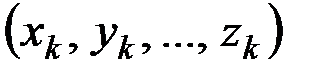 будет соответствовать точка с такой же массой и координатами
будет соответствовать точка с такой же массой и координатами 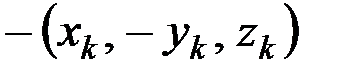 . В результате получим, что
. В результате получим, что  и
и  ,так как в этих суммах все слагаемые попарно одинаковы по модулю и противоположны по знаку, или, согласно равенствам (6.16),
,так как в этих суммах все слагаемые попарно одинаковы по модулю и противоположны по знаку, или, согласно равенствам (6.16),
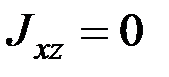 ,
, 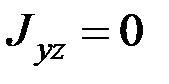 . (6.18)
. (6.18)
Таким образом, симметрия в распределении масс относительно оси 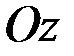 характеризуется обращением в нуль двух центробежных моментов инерции
характеризуется обращением в нуль двух центробежных моментов инерции 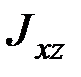 и
и 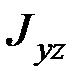 . Ось
. Ось  , для которой центробежные моменты инерции
, для которой центробежные моменты инерции 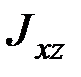 ,
, 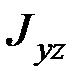 , содержащие в своих индексах наименование этой оси, равны нулю, называется главной осью инерции тела для точки
, содержащие в своих индексах наименование этой оси, равны нулю, называется главной осью инерции тела для точки  .
.
Из изложенного следует, что если тело имеет ось симметрии, то эта ось является главной осью инерции тела для любой своей точки.
Главная ось инерции не обязательно является осью симметрии. Рассмотрим однородное тело, имеющее плоскость симметрии. Проведём в этой плоскости какие-нибудь оси  и перпендикулярную к ним ось
и перпендикулярную к ним ось  . Тогда в силу симметрии каждой точке с массой
. Тогда в силу симметрии каждой точке с массой  и координатами
и координатами 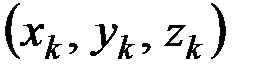 будет соответствовать точка с такой же массой и координатами
будет соответствовать точка с такой же массой и координатами  . В результате, как и в предыдущем случае, найдём, что
. В результате, как и в предыдущем случае, найдём, что 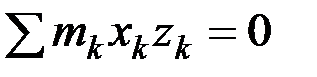 и
и  или
или  ,
, 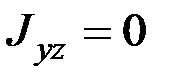 . Следовательно, если тело имеет плоскость симметрии, то любая ось, перпендикулярная этой плоскости, будет главной осью инерции тела для точки
. Следовательно, если тело имеет плоскость симметрии, то любая ось, перпендикулярная этой плоскости, будет главной осью инерции тела для точки  , в которой ось пересекает плоскость.
, в которой ось пересекает плоскость.
Равенства (6.18) выражают условия того, что ось  является главной осью инерции тела для точки
является главной осью инерции тела для точки  (начала координат). Аналогично, если
(начала координат). Аналогично, если  ,
, 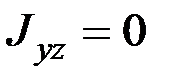 , то ось Оx будет для точки
, то ось Оx будет для точки  главной осью инерции и т.д. Следовательно, если все центробежные моменты инерции равны нулю, т.е.
главной осью инерции и т.д. Следовательно, если все центробежные моменты инерции равны нулю, т.е.
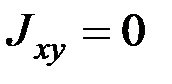 ,
,  ,
, 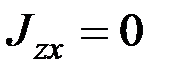 , (6.19)
, (6.19)
то каждая из координатных осей 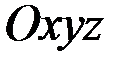 является главной осью инерции тела для точки
является главной осью инерции тела для точки  (начала координат).
(начала координат).
Моменты инерции тела относительно главных осей инерции называются главными моментами инерции тела.
Главные оси инерции, построенные для центра масс тела, называют главными центральными осями инерции тела. Из доказанного выше следует, что если тело имеет ось симметрии, то эта ось является одной из главных центральных осей инерции тела, так как центр масс лежит на этой оси. Если же тело имеет плоскость симметрии, то ось, перпендикулярная этой плоскости и проходящая через центр масс тела, будет также одной из главных центральных осей инерции тела.
В приведённых примерах рассматривались симметричные тела. Однако можно доказать, что через любую точку какого угодно тела можно провести, по крайней мере, три такие взаимно перпендикулярные оси, для которых будут выполняться равенства (6.19), т.е. которые будут главными осями инерции тела для этой точки.
Понятие о главных осях инерции играет важную роль в динамике твёрдого тела. Если по ним направить координатные оси 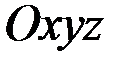 , то все центробежные моменты инерции обращаются в нули, исоответствующие уравнения или формулы существенно упрощаются.
, то все центробежные моменты инерции обращаются в нули, исоответствующие уравнения или формулы существенно упрощаются.
Date: 2015-09-03; view: 752; Нарушение авторских прав