Моменты инерции тела относительно параллельных осей. Теорема Гюйгенса – Штейнера

Моменты инерции данного тела относительно разных осей будут, вообще говоря, разными. Покажем, как, зная момент инерции относительно какой-нибудь одной оси, проведённой в теле, найти момент инерции относительно любой другой оси, ей параллельной.

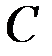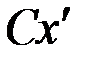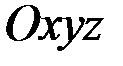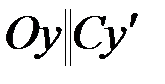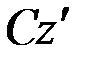Проведём через центр масс тела произвольные оси , а через лю­бую точку на оси – оси ,такие, что , (рис. 20). Расстояние между осями и 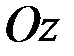обозначим через .

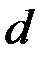Рис. 20

Тогда

,

.

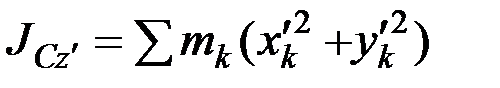Для любой точки тела справедливо равенство

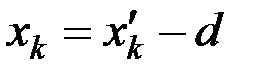
или

;

.

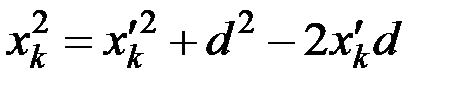Подставив эти значения , 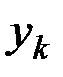в выражение для 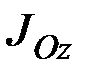,получим

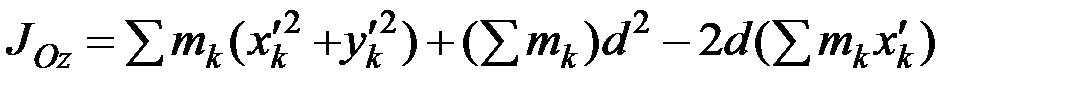. (6.14)

В правой части равенства (6.14) первая сумма равна 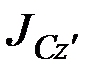, а вторая – массе тела 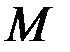. Найдём значение третьей суммы. На основании формул для координат центра масс 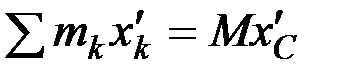. Так как в нашем случае точка 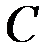является началом координат, то 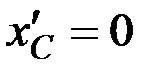и, следовательно, . Окончательно получим:

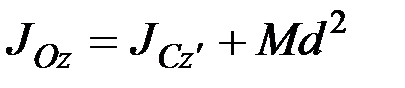. (6.15)

Формула (6.15) выражает теорему Гюйгенса–Штейнера: момент инерции тела относительно данной оси равен моменту инерции относительно оси, ей параллельной, проходящей через центр масс тела, сложенному с произведением массы всего тела на квадрат расстояния между осями.

Из формулы (6.15) следует, что 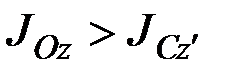. Следовательно, из всех осей данного направления наименьший момент инерции будет относительно той оси, которая проходит через центр масс.

Date: 2015-09-03; view: 616; Нарушение авторских прав