Моменты инерции твёрдого тела относительно осей координат

При поступательном движении твёрдого тела, как и при движении материальной точки, мерой его инертности является масса тела. При вращательном движении твёрдого тела мерой инертности является момент инерции твёрдого тела относительно оси вращения. Поэтому до исследования различных видов движения твёрдого тела следует рассмотреть вычисление моментов инерции твёрдых тел и установить основные теоремы о моментах инерции, имеющие важное значение в динамике твёрдого тела.

Для установления понятий моментов инерции твёрдого тела относительно плоскости, оси и полюса проведём через произвольную точку три взаимно перпендикулярные координатные оси 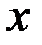, , 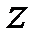и изобразим координатные плоскост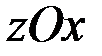и , и (рис. 16). Рассмотрим заданное твёрдое тело как множество материальных точек .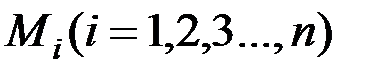

Моментом инерции твёрдого тела относительно плоскости называется скалярная величина, равная сумме произведений массы каждой точки тела на квадрат расстояния от этой точки до плоскости.

Для определения моментов инерции тела относительно координатных плоскостей опустим из каждой точки тела перпендикуляры на плоскости , , :

, , .

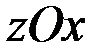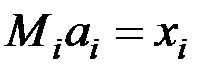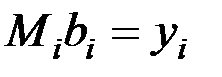Обозначим моменты инерции твёрдого тела относительно координатных плоскостей 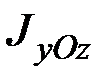, 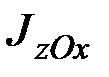и .

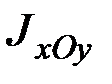Моментом инерции твёрдого тела относительно оси называется скалярная величина, равная сумме произведений массы каждой точки тела на квадрат расстояния от этой точки до оси.

Рис. 16

Для определения моментов инерции твёрдого тела относительно координатных осей опустим из каждой точки тела 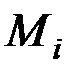на оси 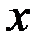, , 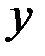перпендикуляры 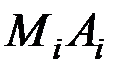, , 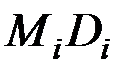. Квадраты этих перпендикуляров равны

,

,

.

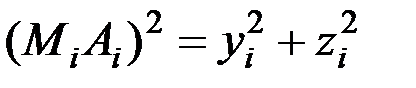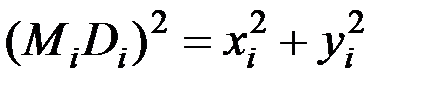Обозначим моменты инерции твёрдого тела относительно координатных осей , , :

,

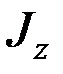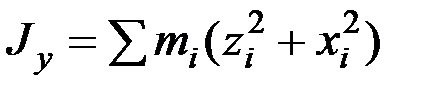, (6.1)

.

Моментом инерции твёрдого тела относительно полюса (полярным моментом инерции) называется скалярная величина, равная сумме произведений массы каждой точки тела на квадрат расстояния от точки до этого полюса.

Обозначим 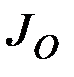момент инерции твёрдого тела относительно полюса :

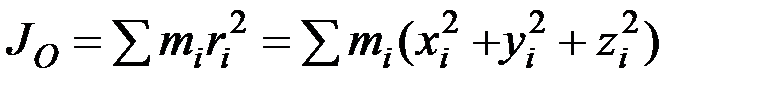. (6.2)

Между моментами инерции твёрдого тела относительно координатных плоскостей, координатных осей и начала координат существуют следующие зависимости:

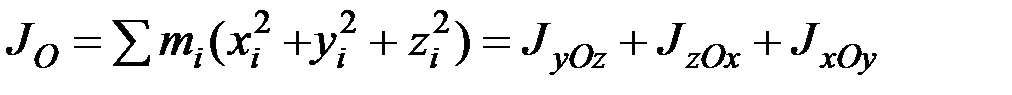, (6.3)

, (6.4)

откуда

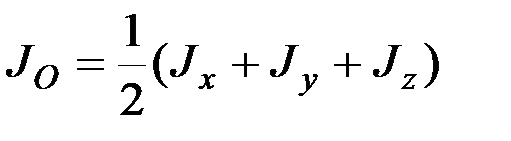, (6.5)

где

,

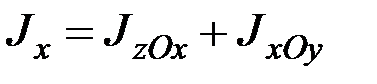, (6.6)

.

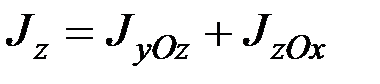Эти зависимости используются при вычислении моментов инерции твёрдых тел.

Момент инерции твёрдого тела относительно заданной оси, например оси , можно представить в виде произведения массы тела на квадрат линейной величины, называемой радиусом инерции тела относительно этой оси:

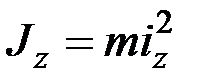, (6.7)

где 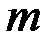– масса тела, – радиус инерции тела относительно оси.

Формула (6.7) показывает, что радиус инерции определяет расстояние от оси 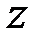до точки, в которой нужно сосредоточить всю массу тела, чтобы момент инерции точки относительно этой оси был равен моменту инерции тела. Момент инерции твёрдого тела относительно оси как сумма положительных слагаемых всегда положителен и не может быть равен нулю.

Единицей момента инерции в системе СИ является , а в системе . В технической системе единиц МКГСС за единицу момента инерции принимается .

Найдём моменты инерции некоторых однородных тел.

Тонкий однородный стержень длины l и массы М. Вычислим его момент инерции относительно оси 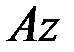, перпендикулярной стержню (рис. 17).

Рис. 17

Направим вдоль 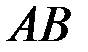координатную ось . Воспользуемся одной из формул (6.1) в интегральной форме:

.

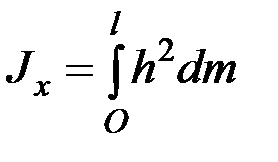Тогда для любого элементарного отрезка длины величина 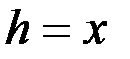, а масса 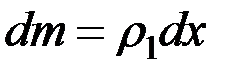,где – масса единицы длины стержня. В результате

.

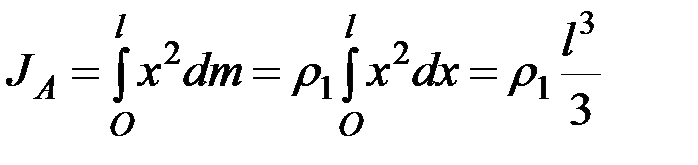Заменив здесь 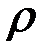его значением, найдём окончательно:

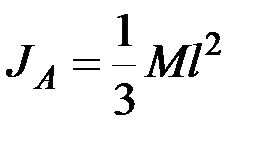. (6.8)

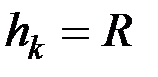Тонкое круглое однородное кольцо радиусом R и массой M. Найдём его момент инерции относительно оси ,перпендикулярной плоскости кольца и проходящей через его центр (рис. 18, а). Так как все точки кольца находятся от оси на расстоянии ,то

. (6.9)

Следовательно, для кольца момент инерции будет равен:

.

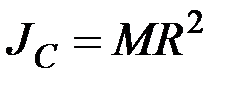Очевидно, такой же результат получится для момента инерции тонкой цилиндрической оболочки массы М и радиуса R относительно ее оси.

Круглая однородная пластина или цилиндр радиусом R и массой М. Вычислим момент инерции круглой пластины относительно оси 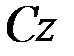, перпендикулярной к пластине и проходящей через ее центр. Для этого выделим элементарное кольцо радиусом ишириной (рис 18, б).

Рис. 18

Площадь этого кольца равна 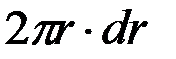,а масса 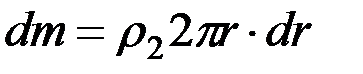,где 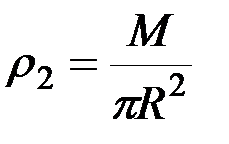– масса единицы площади пластины. Тогда для выделенного элементарного кольца момент инерции будет равен:

,

а для всей пластины –

.

Заменив r₂ его значением, найдём окончательно

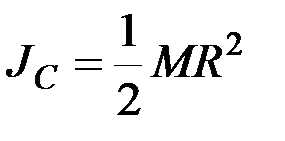. (6.10)

Моменты инерции однородного шара. Масса шара радиусом и плотностью 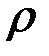(рис. 19) равна:

. (6.11)

Рис. 19

Для определения момента инерции шара относительно центральной оси разобьём его на множество элементарных пластинок толщиной , параллельных плоскости . Масса пластинки радиусом 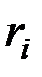равна:

.

Момент инерции элементарной пластинки относительно оси :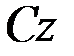

;

.

Момент инерции шара относительно оси получим, суммировав моменты инерции элементарных пластинок и перейдя к пределу суммы:

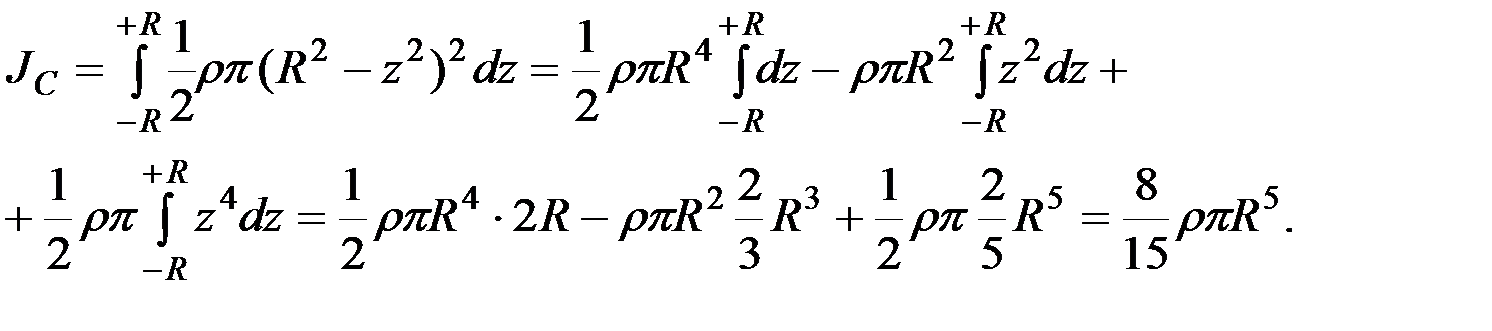(6.12)

После подстановки равенства (6.11) в (6.12) получим:

. (6.13)

Так как оси 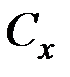, , проведены по диаметрам шара, то

.

Date: 2015-09-03; view: 829; Нарушение авторских прав