Свободные колебания точки без учёта сил сопротивления

Рассмотрим точку M,движущуюся прямолинейно под действием одной только восстанавливающей силы ,направленной к неподвижному центру O и пропорциональной расстоянию от этого центра. Проекция силы F на ось Ox (рис. 6)будет равна

.

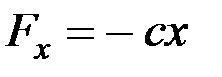Рис. 6

Сила F,как видим, стремится вернуть точку в равновесное положение O, где x = 0, отсюда и название восстанавливающей силы.

Найдём закон движения точки M. Составив дифференциальное уравнение движения, получим

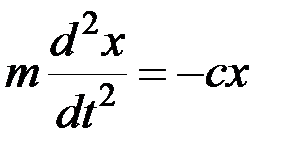. (3.1)

Поделив обе части равенства на m и введя обозначение

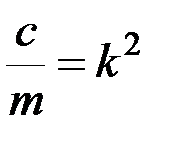, (3.2)

приведем уравнение к виду:

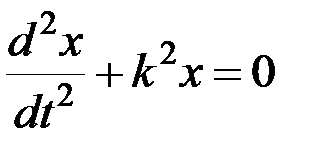. (3.3)

Уравнение (3.3) представляет собой дифференциальное уравнение свободных колебаний при отсутствии сопротивления. Решение этого линейного однородного дифференциального уравнения второго порядка определяют в виде 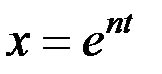. Полагая в уравнении (3.3) 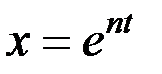,получим для определения п так называемое характеристическое уравнение, имеющее в данном случае вид 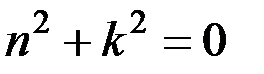. Поскольку корни этого характеристического уравнения являются мнимыми 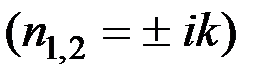, то, как известно из теории дифференциальных уравнений, общее решение уравнения (3.3) примет вид:

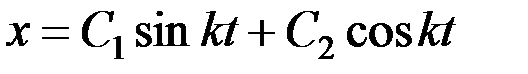, (3.4)

где C ₁ и C ₂ – постоянные интегрирования. Если вместо постоянных C ₁ и C ₂ ввести постоянные 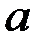и 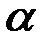, для которых должны выполняться следующие условия:

, ,

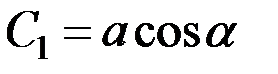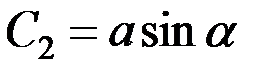то получим

или

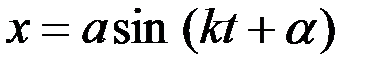. (3.5)

Скорость точки в рассматриваемом движении равна

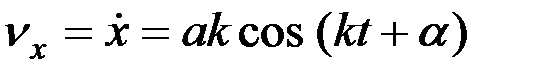. (3.6)

Колебания, совершаемые точкой по закону (3.5), называются гармоническими колебаниями. Величина a, равная наибольшему отклонению точки M от центра колебаний, называется амплитудой колебаний. Величина 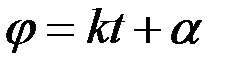называется фазой колебаний. Фаза 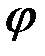, в отличие от координаты x, определяет не только положение точки в данный момент, но и направление ее последующего движения: например, из положения M при фазе, равной 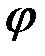, точка движется вправо, а при фазе, равной 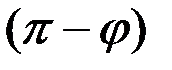– влево. Фазы, отличающиеся на 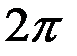, считаются одинаковыми. Величина 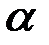определяет фазу начала колебаний (начальная фаза). Например, при 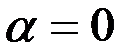колебания происходят по закону синуса; при 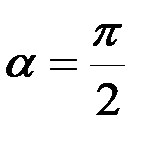– начинаются из положения x = a со скоростью 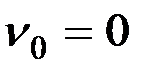(по закону косинуса). Величина k, совпадающая с угловой скоростью вращения, называется круговой частотой колебаний.

Промежуток времени T (или 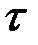), в течение которого точка совершает одно полное колебание, называется периодом колебаний. По истечении периода фаза изменяется на . Следовательно, должно быть 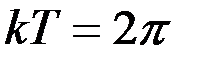,откуда период равен

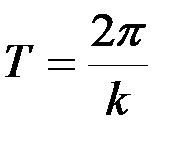. (3.7)

Величина 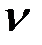, обратная периоду и определяющая число колебаний, совершаемых за одну секунду, называется частотой колебаний:

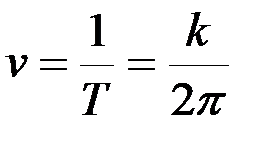. (3.8)

Отсюда видно, что величина 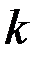отличается от 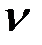только постоянным множителем .

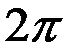Отметим, что свободные колебания при отсутствии сопротивления обладают следующими свойствами:

1) амплитуда и начальная фаза колебаний зависят от начальных условий;

2) частота k,а следовательно, и период T колебаний от начальных условий не зависят.

3.3. Свободные колебания при сопротивлении,
пропорциональном скорости (затухающие колебания)

Рассмотрим, как влияет на свободные колебания сопротивление среды, считая, что сила сопротивления пропорциональна первой степени скорости:

,

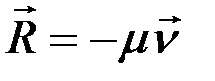где знак «–» указывает, что сила 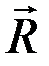направлена противоположно .

Пусть на точку при ее движении действуют восстанавливающая сила 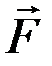и сила сопротивления 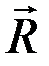(рис. 7).

Рис. 7

Тогда , ,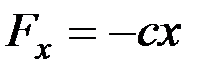

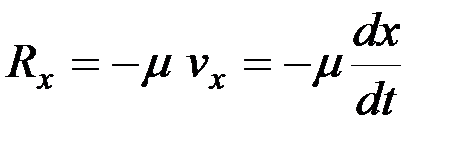и дифференциальное уравнение движения будет иметь вид:

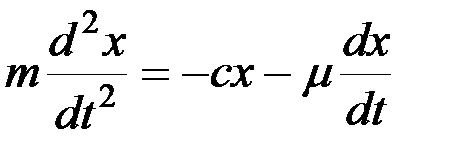. (3.9)

Поделив обе части уравнения на m, получим:

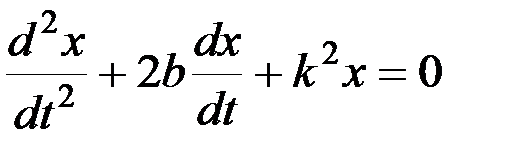, (3.10)

где обозначено

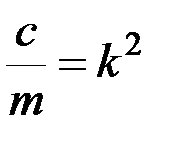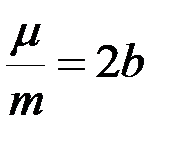, . (3.11)

При этом легко проверить, что величины и 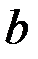имеют одинаковые размерности (1/ c).Это позволяет сравнивать их друг с другом. Уравнение (3.10) представляет собой дифференциальное уравнение свободных колебаний при сопротивлении, пропорциональном скорости. Его решение, как и решение уравнения (3.3), ищут в виде х = е^nt. Подставив это значение 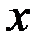в уравнение (3.10), получим характеристическое уравнение 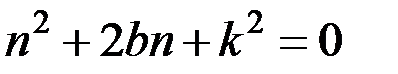, корни которого будут равны:

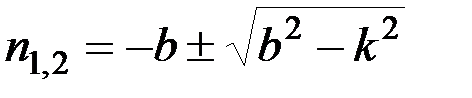. (3.12)

Рассмотрим случай, когда ,т. е. сопротивление по сравнению с восстанавливающей силой мало. Введя обозначение

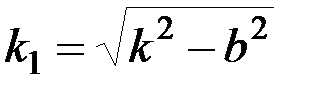, (3.13)

получим из уравнения (3.12), что

,

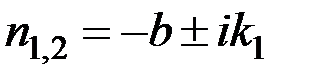т.е. корни характеристического уравнения являются комплексными. Тогда общее решение уравнения (3.10) будет отличаться от решения уравнения (3.3) только множителем 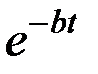,т. е. будет иметь вид:

(3.14)

или, по аналогии с равенством (3.5),

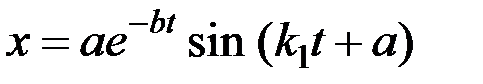. (3.15)

Входящие в уравнение (3.15) величины 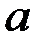и 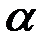являются постоянными интегрирования и определяются по начальным условиям.

Колебания, происходящие по закону (3.15), называют затухающими, так как благодаря наличию множителя 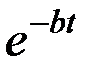величина 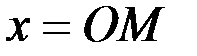с течением времени убывает, стремясь к нулю. График этих колебаний показан на рис. 8 (график заключен между пунктирными кривым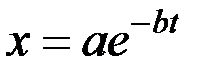и и 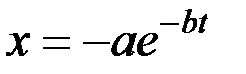, так как 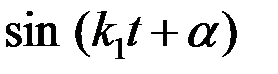по модулю не может стать больше единицы).

Рис. 8

Промежуток времени 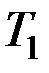,равный периоду 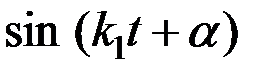, т. е величину

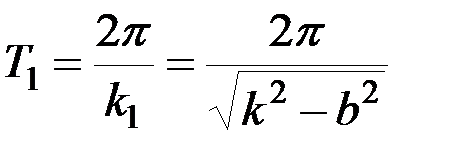, (3.16)

принято называть периодом затухающих колебаний. За период точка совершает одно полное колебание, т. е., например, начав двигаться из положения 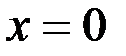вправо (рис. 7), приходит в то же положение, также двигаясь вправо. Формулу (3.16), если учесть равенство (3.7), можно представить в виде:

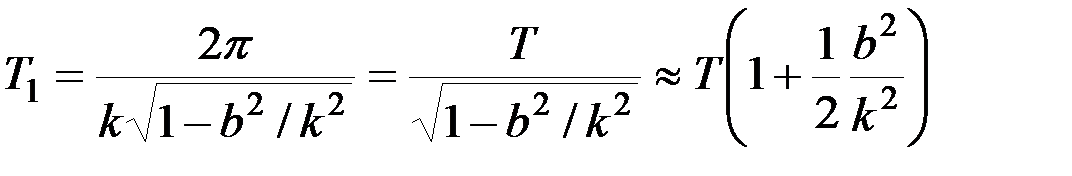. (3.17)

Из полученных формул видно, что 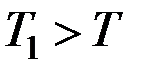, т.е. наличие сопротивления несколько увеличивает период колебаний. Однако, когда сопротивление мало 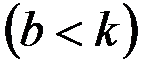,величиной 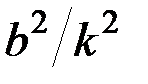по сравнению с единицей можно пренебречь и считать 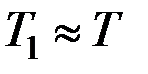. Следовательно, малое сопротивление на период колебаний практически не влияет.

Промежуток времени между двумя последовательными отклонениями колеблющейся точки вправо (или влево) также оказывается равным .

Моменты, когда х имеет максимум или минимум, определяются из уравнения

.

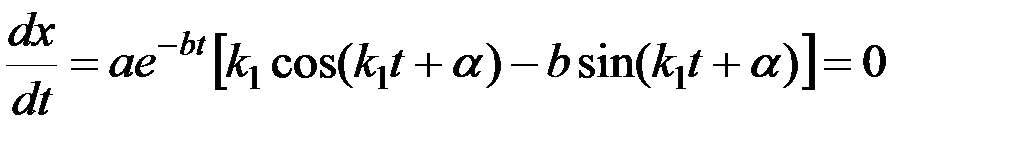Если квадратная скобка обращается в нуль при некотором 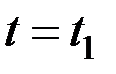,то она обратится в нуль и в моменты 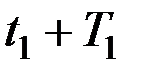, 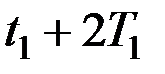и т.д., поскольку .

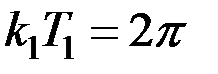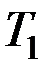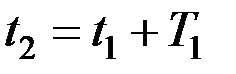Следовательно, если первое максимальное отклонение вправо происходит в момент времени , то второе отклонение наступит в момент и т. д. Тогда по формуле (3.15), учитывая, что 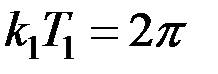, получим:

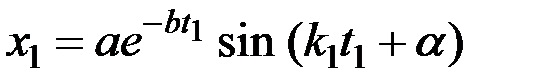, (3.18)

.

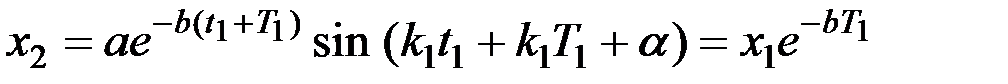Аналогично для любого отклонения будет 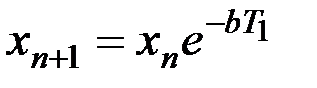. Таким образом, оказывается, что размахи колебаний будут убывать по закону геометрической прогрессии. Знаменатель этой прогрессии 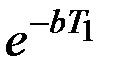называется декрементом рассматриваемых колебаний, а модуль его логарифма, т.е. величина ,– логарифмическим декрементом.

Из полученных результатов следует, что малое сопротивление почти не влияет на период колебаний, но вызывает постепенное их затухание вследствие убывания размахов колебаний по закону геометрической прогрессии.

В заключение рассмотрим случай, когда ,т.е. сопротивление по сравнению с восстанавливающей силой велико. Вводя обозначение 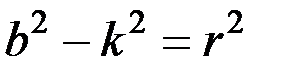, найдём, что в этом случае корни характеристического уравнения (3.12) равны 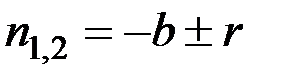,т.е. оба действительны и отрицательны (так как 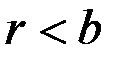). Следовательно, решение уравнения (3.10), описывающее закон движения точки, при имеет вид:

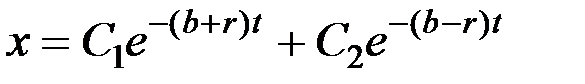. (3.19)

Поскольку функция 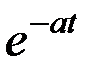(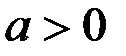) со временем монотонно убывает, стремясь к нулю, то движение точки в этом случае не будет колебательным, и она под действием восстанавливающей силы будет постепенно приближаться к равновесному положению .

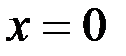График такого движения (если при 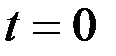, , 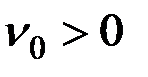) показан на рис. 9.

Рис. 9

Date: 2015-09-03; view: 978; Нарушение авторских прав