Движение несвободной материальной точки. Связи и динамические реакции связей

Несвободной материальной точкой называется точка, свобода движения которой ограничена.

Тела, ограничивающие свободу движения точки, называются связями.

Пусть связь представляет собой поверхность какого-либо тела, по которой движется точка. Тогда координаты точки должны удовлетворять уравнению этой поверхности, называемому уравнением связи:

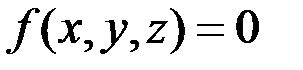. (4.1)

Аналогично, если точка вынуждена двигаться по некоторой линии (движение шарика внутри криволинейной трубки), то уравнениями связи являются уравнения этой линии:

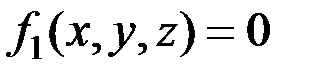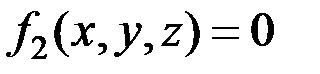; . (4.2)

Таким образом, движение несвободной материальной точки зависит не только от приложенных к точке активных сил и начальных условий, но и от имеющихся связей. При этом значения начальных условий не могут быть независимыми друг от друга, а должны удовлетворять уравнениям связей.

Переходя к классификации механических связей, отметим прежде всего деление связей на двусторонние, или удерживающие, и на односторонние, или неудерживающие,связи.

Связь называется двусторонней, если накладываемые ею на координаты точки ограничения выражаются в форме равенств, определяющих кривые или поверхности в пространстве, на которых должна находиться эта точка.

Двусторонняя, или удерживающая, связь препятствует перемещению точки тела в двух противоположных направлениях.

Ограничения, накладываемые на координаты точки односторонней связью, выражаются неравенствами. Односторонняя связь препятствует перемещению точки (тела) лишь в одном направлении и допускает её перемещение в других направлениях. Примером односторонней связи может служить тяжелый шарик 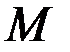,привязанный к нити 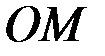,закреплённой в точке . Он может находиться не только на поверхности сферы радиусом 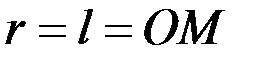, но и внутри сферы (рис. 11).

Движение шарика внутри является свободным до тех пор, пока он не удалится от неподвижной точки на расстояние, равное длине нити.

Рис. 11

Рассмотренная связь имеет уравнение

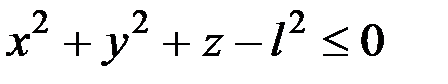. (4.3)

Примером односторонней связи также может служить горизонтальная плоскость (рис. 12, а), которая препятствует перемещению шарика только вертикально вниз.

Рис. 12

Примером двусторонней связи может служить совокупность двух горизонтальных плоскостей (рис. 12, б),которые препятствуют перемещению шарика как вниз, так и вверх по вертикали.

Ниже рассматриваются лишь двусторонние, или удерживающие, связи, которые подразделяются на конечные и дифференциальные в зависимости от того, является равенство, их выражающее, конечным соотношением или дифференциальным уравнением вида

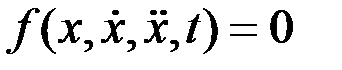. (4.4)

В том случае, если связи выражаются дифференциальными уравнениями, которые могут быть проинтегрированы, они называются дифференциальными интегрируемыми связями.

Связь называется неголономной, если дифференциальное уравнение, выражающее связь, неинтегрируемое, т.е. его нельзя привести к некоторому эквивалентному соотношению между координатами точки и временем:

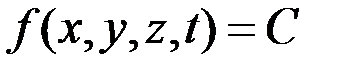(4.5)

В зависимости от того, входят ли в это уравнение только первые или вторые производные от координат, неголономная связь может быть первого или второго порядка.

Связь называется голономной, если она выражается или конечным соотношением между координатами точки (т.е. уравнением, не содержащим никаких производных от координат) или интегрируемым дифференциальным уравнением.

Ниже рассматриваются лишь голономные механические связи, которые, в свою очередь, разделяются на связи стационарные и нестационарные.

В том случае, если равенства, выражающие связи, не содержат явно время, их называют стационарными, а если в эти равенства явно входит время – нестационарными.

Примером голономной двусторонней стационарной связи может служить абсолютно жёсткий стержень 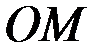длиной , соединяющий материальную точку с неподвижной точкой (рис. 13).

Рис. 13

Стержень 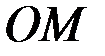ограничивает движение точки, допуская ее движение лишь по сферической поверхности радиусом .

Уравнение связи имеет вид:

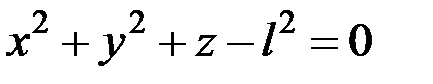. (4.6)

Уравнение (4.6) связывает координаты точки и не содержит времени.

Если материальная точка движется по окружности радиусом с центром в начале координат и окружность расположена в плоскости 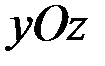,то уравнение связи имеет вид:

; .

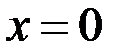Рассмотрим пример односторонней нестационарной связи: материальную точку 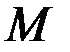,прикреплённую к концу нерастяжимой и невесомой нити 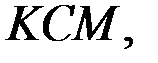проходящей через неподвижное кольцо 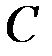(рис. 14).

Рис. 14

Если конец нити 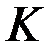перемещается с постоянной скоростью 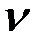,то длина нити 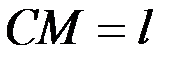изменяется с течением времени согласно уравнению

,

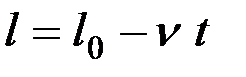где – длина 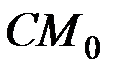в начальный момент.

Если нить остается в одной системе координат 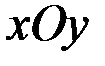, то

,

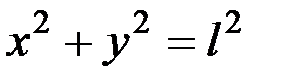или

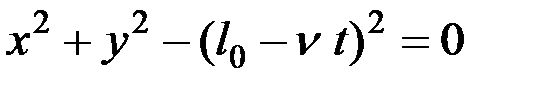. (4.7)

Для каждого момента времени уравнение связи определяет окружность, но с течением времени радиус этой окружности уменьшается. Таким образом, точка 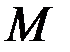должна находиться на окружности, стягивающейся с течением времени в точку. В этом случае уравнение связи

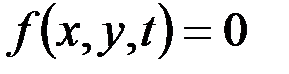, (4.8)

кроме координат 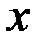и 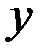,содержит время .

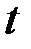Неравенства, соответствующие неудерживающей нестационарной связи, имеют общий вид

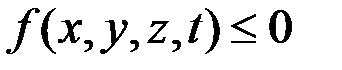
или (4.9)

.

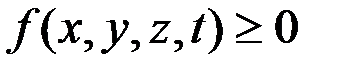Все силы, действующие на несвободную материальную точку или несвободное тело, делят на задаваемые (активные) силы и реакции связей. Задаваемые силы выражают действие на материальную точку некоторых тел, вызывающих или стремящихся вызвать определённое её движение.

Реакции связей выражают действие связей, ограничивающих движение материальной точки или препятствующих ему.

При изучении движения несвободной материальной точки применяют принцип освобождаемости точки от связей, используемый в курсе статики. Этот принцип позволяет рассматривать движение несвободной материальной точки как движение свободной точки под действием задаваемых сил и реакций связей.

Контрольные вопросы

1. Под действием какой силы совершаются свободные колебания материальной точки?

2. Какой вид имеет дифференциальное уравнение свободных колебаний материальной точки?

3. От каких факторов зависят частота, период, амплитуда и начальная фаза колебаний?

4. Какой вид имеет дифференциальное уравнение вынужденных колебаний материальной точки, и каково его общее решение?

5. Каковы частота и период вынужденных колебаний материальной точки?

6. При каких условиях возникает резонанс, и каковы уравнение и график вынужденных колебаний материальной точки при резонансе?

7. Что называется связью?

8. Какие связи называются стационарными и нестационарными?

Date: 2015-09-03; view: 786; Нарушение авторских прав