ЗАКОНЫ ГАЛИЛЕЯ–НЬЮТОНА

Динамикой называется раздел механики, в котором изучаются законы движения материальных тел под действием сил.

Движение тел с чисто геометрической точки зрения было изучено в кинематике. В динамике, в отличие от кинематики, при изучении движения тел принимают во внимание и действующие силы, и инертность самих материальных тел.

Понятие о силе, как о величине, характеризующей меру механического взаимодействия материальных тел, было введено в статике. Но при этом в статике мы, по существу, считали все силы постоянными и не касались вопроса о возможных изменениях этих сил с течением времени. Между тем, на движущееся тело наряду с постоянными силами (постоянной, например, можно считать силу тяжести) действуют обычно силы переменные, модули и направления которых при движении тела изменяются. При этом переменными могут быть и заданные (активные) силы, и реакции связей.

Как показывает опыт, переменные силы могут определённым образом зависеть от времени, от положения тела и от его скорости. В частности, от времени зависит сила тяги электровоза при постепенном выключении или включении реостата или сила, вызывающая колебания фундамента при работе мотора с плохо центрированным валом; от положения тела зависит ньютонова сила тяготения или сила упругости пружины; от скорости движения зависят силы сопротивления среды (воды, воздуха). Такие именно силы, наряду с постоянными, и будут рассматриваться в динамике. Законы сложения или приведения переменных сил остаются теми же, что и для сил постоянных.

К понятию об инертности тел мы приходим, сравнивая результаты действия одной и той же силы на разные материальные тела. Опыт показывает, что если одну и ту же силу приложить к двум разным, свободным от других воздействий покоящимся телам, то в общем случае по истечении одного и того же промежутка времени эти тела пройдут разные расстояния и будут иметь разные скорости.

Инертность и представляет собой свойство материальных тел быстрее или медленнее изменять скорость своего движения под действием приложенных сил. Если, например, при действии одинаковых сил изменение скорости первого тела происходит медленнее, чем второго, то говорят, что первое тело является более инертным, и наоборот. Большая или меньшая степень инертности данного тела зависит от количества заключённого в нём вещества (материи).

Величина, зависящая от количества вещества данного тела и определяющая меру его инертности, называется массой тела. В механике масса т рассматривается как величина скалярная, положительная и постоянная для каждого данного тела.

В общем случае характер движения тела зависит не только от его суммарной массы и приложенных сил, но и от геометрических размеров тела и взаимного расположения образующих его частиц (т.е. от распределения масс).

Для того чтобы при первоначальном изучении динамики иметь возможность отвлечься от учёта влияния размеров тел и распределения масс, вводится понятие о материальной точке.

Материальной точкой называется материальное тело (тело, имеющее массу), размерами которого при изучении его движения можно пренебречь.

Естественно, чтоизучение движения одной материальной точки должно предшествовать изучению движения системы точек и, в частности, твёрдого тела. Поэтому курс динамики принято обычно разделять на динамику точки и динамику системы материальных точек.

В основе динамики лежат законы, установленные путём обобщения результатов целого ряда опытов и наблюдений над движением тел и проверенные обширной общественно-исторической практикой человечества.

Это законы, сформулированные Ньютоном и названные им аксиомами или законами движения (Axiomata sive leges motus).

1. Закон инерции.

2. Закон пропорциональности силы и ускорения.

3. Закон равенства действия и противодействия.

4.Закон независимости действия сил.

Первый закон (закон инерции), открытый Галилеем (1638 г.), гласит: изолированная от внешних воздействий материальная точка сохраняет своё состояние покоя или равномерного прямолинейного движения до тех пор, пока приложенные силы не заставят ее изменить это состояние. Движение, совершаемое точкой при отсутствии сил, называется движением по инерции.

Закон инерции отражает одно из основных свойств материи – пребывать неизменно в движении – и устанавливает для материальных тел эквивалентность состояний покоя и движения по инерции. Из него следует, что если F = 0, то точка покоится или движется с постоянной по модулю и направлению скоростью (V = const); ускорение точки при этом равно нулю (a = 0); если движение точки не является равномерным и прямолинейным, то на точку действует сила.

Система отсчёта, по отношению к которой выполняется закон инерции, называется инерциальной системой отсчёта (иногда её условно называют неподвижной). По данным опыта, для нашей Солнечной системы инерциальной является система отсчета, начало которой находится в центре Солнца, а оси направлены на так называемые неподвижные звезды. При решении большинства технических задач инерциальной (с достаточной для практики точностью) можно считать систему отсчёта, жёстко связанную с Землей.

Второй закон (основной закон динамики) устанавливает, как изменяется скорость точки при действии на неё какой-нибудь силы. Он гласит: произведение массы точки на ускорение, которое она получает под действием данной силы, равно по модулю этой силе, а направление ускорения совпадает с направлением силы.

Математически этот закон выражается векторным равенством

. (1.1)

При этом между модулями ускорения и силы существует зависимость:

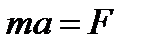. (1.2)

Второй закон динамики, как и первый, применяется только по отношению к инерциальной системе отсчёта. Из этого закона непосредственно видно, что мерой инертности материальной точки является её масса, так как две разные точки при действии одной и той же силы получают одинаковые ускорения только тогда, когда равны их массы; если же массы будут разные, то точка, масса которой больше (т. е. более инертная), получит меньшее ускорение, и наоборот.

Если на точку действует одновременно несколько сил, то они, как известно, будут эквивалентны одной силе, т. е. равнодействующей R, равной геометрической сумме этих сил. Уравнение, выражающее основной закон динамики, принимает в этом случае вид:

. (1.3)

Этот же результат можно получить, используя вместо аксиомы параллелограмма закон независимости действия сил, согласно которому при одновременном действии на точку нескольких сил каждая из них сообщает точке такое же ускорение, какое она сообщила бы, действуя одна.

Вес тела и его масса. На все тела, находящиеся вблизи земной поверхности, действует сила тяжести P,численно равная весу тела. Опытом установлено, что под действием силы P любое тело при свободном падении на Землю (с небольшой высоты и в безвоздушном пространстве) имеет одно и то же ускорение g. Это ускорение, сообщаемое телу силой тяжести, называют для краткости ускорением силы тяжести или ускорением свободного падения. Для этого движения на основании уравнения (1.2) имеем:

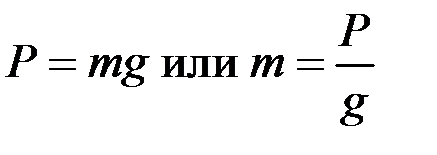. (1.4)

Равенство (1.4) позволяет, если известна масса тела, определить его вес, и наоборот; оно устанавливает, что вес тела равен его массе, умноженной на ускорение силы тяжести, или масса тела равна его весу, делённому на ускорение силы тяжести. Вес тела, как и величина g,изменяется с изменением широты и высоты над уровнем моря; масса же является величиной, для данного тела (или материальной точки) неизменной.

Третий закон (закон равенства действия и противодействия) устанавливает характер механического взаимодействия между материальными телами. Для двух материальных точек он формулируется следующим образом: две материальные точки действуют друг на друга с силами, равными по модулю и направленными вдоль прямой, соединяющей эти точки, в противоположные стороны.

Для свободной материальной точки задачами динамики являются следующие: 1) зная закон движения точки, определить действующую на нее силу (первая задача динамики);2) зная действующие на точку силы, определить закон движения точки (вторая или основная задача динамики). Решаются эти задачи с помощью уравнений (1.1) или (1.3), выражающих основной закон динамики, так как эти уравнения связывают ускорение a,т. е. величину, характеризующую движение точки, и действующие на неё силы.

В технических дисциплинах изучается несвободное движение точки, т.е. случаи, когда точка, благодаря наложенным на нее связям, вынуждена двигаться по заданной неподвижной поверхности или кривой. В этих случаях, как и в статике, при решении задач следует исходить из аксиомы связей, согласно которой всякую несвободную материальную точку можно рассматривать как свободную, отбросив связь и заменив ее действие реакцией этой связи 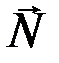. Тогда основной закон динамики для несвободного движения точки примет вид:

, (1.5)

где – действующие на точку активные силы.

Первая задача динамики для несвободного движения сводится к тому, чтобы, зная движение точки и действующие на нее активные силы, определить реакцию связи. Вторая (основная) задача динамики при несвободном движении распадается на две и состоит в том, чтобы, зная действующие на точку активные силы, определить: а) закон движения точки, б) реакцию наложенной связи.

Четвертый закон – закон независимости действия сил – не был сформулирован Ньютоном как отдельный закон механики, но он содержится в сделанном им обобщении правила параллелограмма сил. Положим, что на материальную точку M действуют силы 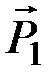, , 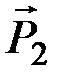…, (рис. 1).

Рис. 1

Каждая из этих сил, действуя на материальную точку отдельно, сообщает ей ускорения , , 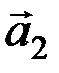…, , 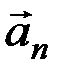определяемые по второму закону:

, , …, .

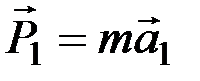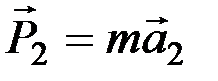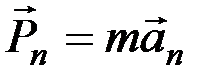Согласно четвертому закону, ускорение материальной точки, нахо­дящейся под действием сил 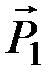, , 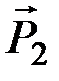…, , определяется уравнением:

.

Подставив в это уравнение значения сил, определяемые по второму закону, получим

.

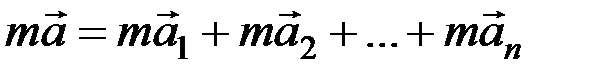Разделив обе части равенства на т, получим

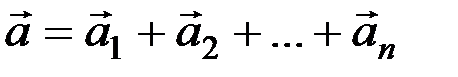. (1.6)

Таким образом, закон независимости действия сил равносилен утверждению, что ускорение , получаемое материальной точкой от одновременно действующей на неё системы сил, равно геометрической сумме ускорений , , 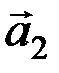…, , сообщаемых этой точке каждой из сил в отдельности.

Четвертый закон, как и остальные законы классической механики, подтверждается опытами и наблюдениями.

Date: 2015-09-03; view: 9735; Нарушение авторских прав