Прямолинейное движение точки

Рассмотрим движение точки в одномерном пространстве.

Пусть на точку действует постоянная по модулю и направлению сила Q. Тогда первое из уравнений (2.3) принимает вид:

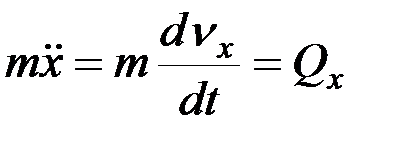. (2.4)

Так как 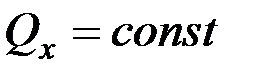, то, умножив обе части уравнения на dt и взяв от них интегралы, получим:

. (2.5)

Так как 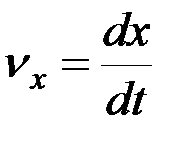, то

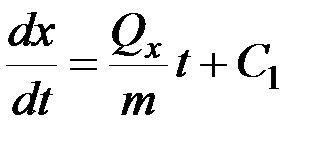. (2.6)

Умножив обе части этого уравнения на dt ипроинтегрировав, найдём:

. (2.7)

Полученный результат и представляет собою для данной задачи общее решение уравнения (2.4).

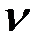Теперь определим постоянные интегрирования C ₁ и C ₂, считая, что в данной задаче имеют место начальные условия: при t = 0, x = x ₀, _x = ₀. Решения (2.5) и (2.7) должны быть справедливы в любой момент времени, в том числе и в момент t = 0. Поэтому, подставив в равенства уравнений (2.5) и (2.7) вместо t нуль, мы вместо _x и x должны получить ₀и x ₀,т.е.:

, .

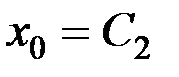Полученными равенствами определяются значения постоянных C ₁ и C ₂, удовлетворяющие начальным условиям данной задачи. Подставив эти значения в уравнение (2.7), окончательно найдём закон происходящего движения в виде:

. (2.8)

Как видно из уравнения (2.8), точка под действием постоянной силы совершает равнопеременное движение, что можно было определить заранее, так как если Q = const, то и a = const. В частности, таким является движение точки под действием силы тяжести. При этом в уравнении (2.8) будет 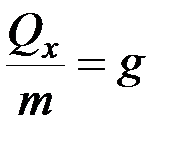,а ось Ox должна быть направлена по вертикали вниз.

Действие на точку системы плоских или пространственных сил приводит к криволинейному движению.

Date: 2015-09-03; view: 1009; Нарушение авторских прав