Ортогональные и ортонормированные базисы

Определение 3.5. Два вектора евклидового пространства называются ортогональными, если их скалярное произведение равно нулю:

.

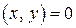Из определения скалярного произведения следует, что нулевой вектор ортогонален любому вектору .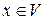

Определение 3.6. Вектор 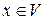называется ортогональным подпространству 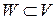, если он ортогонален каждому вектору этого подпространства.

Если 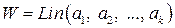, то вектор 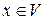ортогонален подпространству 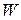тогда и только тогда, когда .

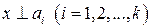Определение 3.7. Система векторов 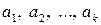евклидова пространства называется ортогональной, если любые её два вектора ортогональны:

, , .

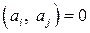Теорема 3.5. Любая ортогональная система 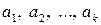ненулевых векторов линейно независима.

□ Составим равенство

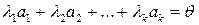, (3.9)

где некоторые действительные числа. Умножив равенство (3.9) скалярно на вектор , на основании свойств скалярного произведения получим:

,

откуда

.

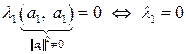Так как 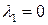, то равенство (3.9) примет вид

, (3.10)

Умножив равенство (3.10) скалярно на вектор 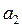, получим . И так далее. Окончательно получаем, что все коэффициенты 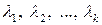равны нулю. Тогда по определению система ненулевых векторов 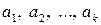линейно независима. ■

Теорема 3.6. Если 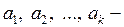ортогональная система векторов, то выполняется равенство

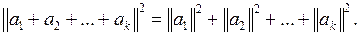(3.11)

□ Вычислим скалярный квадрат вектора :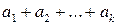

,

откуда и следует равенство (3.11). ■

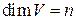Пусть далее – конечномерное () евклидово пространство.

Определение 3.8. Если базис евклидова пространства представляет собой ортогональную систему векторов:

, , ,

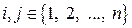то он называется ортогональным базисом евклидова пространства .

Определение 3.9. Вектор называется единичным, если его евклидова норма равна единице:

.

Очевидно, что любой ненулевой вектор можно преобразовать в единичный вектор следующим образом:

.

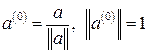При этом говорят, что вектор пронормирован, а число 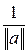называют нормирующим множителем.

Определение 3.10. Ортогональный базис 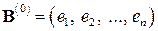евклидова пространства называется ортонормированным, если каждый вектор 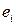(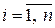) этого базиса – единичный, то есть

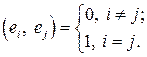
Использование ортонормированного базиса облегчает вычисление скалярного произведения в координатной форме. Пусть 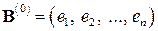– ортонормированный базис и разложение векторов в этом базисе имеет вид

где 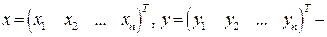координатные вектор-столбцы.

Матрица Грама для системы векторов в этом случае имеет вид

.

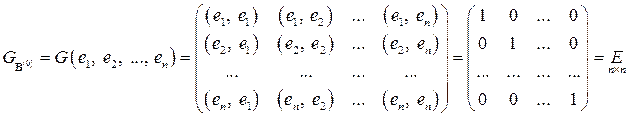Тогда скалярное произведение (3.5) в ортонормированном базисе примет наиболее простой вид

. (3.12)

В ортонормированном базисе также упрощается вычисление координат вектора – они вычисляются через скалярные произведения. Если разложение вектора по ортонормированному базису 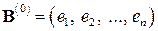имеет вид

,

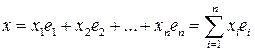то умножив обе части последнего равенства скалярно на (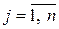), получим

.

Тогда разложение вектора по ортонормированному базису будет иметь вид

.

Date: 2015-09-03; view: 566; Нарушение авторских прав