Примеры евклидовых пространств

Пусть задано линейное пространство. Возникает вопрос: можно ли измерять расстояние между элементами (векторами) этого пространства, находить углы между векторами и длины (модули) этих векторов. Ответы на этот вопрос дает понятие евклидова линейного пространства.

Определение 3.1. Если в линейном пространстве любым двум элементам 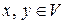можно поставить в соответствие действительное число 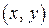, называемое скалярным произведением векторов и удовлетворяющее аксиомам:

,

, ,

, ,

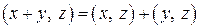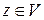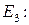
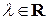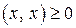, причем ,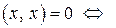

то это пространство называется евклидовым пространством.

Число называется скалярным квадратом вектора .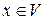

Аксиома определяет симметричность скалярного произведения, аксиомы 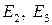– аддитивность и однородность по первому множителю, 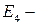неотрицательность скалярного квадрата.

Поскольку евклидово пространство является линейным, то на него переносятся все понятия, определенные для линейного пространства. В частности, можно ввести понятие базиса и размерности евклидова пространства. Сформулируем простейшие следствия из аксиом евклидова пространства:

1) , ,

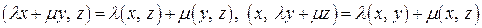2) ,

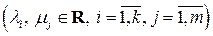3) .

Теорема 3.1. В евклидовом пространстве 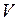для любых двух векторов 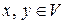справедливо неравенство Коши-Буняковского:

. (3.1)

□ Отбрасывая тривиальный случай, когда один из векторов 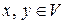нулевой (в этом случае неравенство (3.1) выполняется), предположим, что 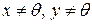. Рассмотрим при произвольном числе 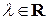вектор и найдем его скалярный квадрат

.

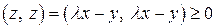Преобразовав скалярное произведение согласно аксиомам, получим

.

Левую часть полученного неравенства можно рассматривать как квадратный трехчлен относительно 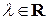(), принимающий неотрицательные значения при каждом 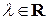. Тогда его дискриминант должен быть неположительным, то есть

,

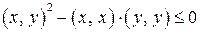откуда и следует неравенство (3.1). ■

В данном пункте приведены примеры наиболее часто встречающихся евклидовых пространств. Заметим, что в одном и том же линейном пространстве скалярное произведение можно ввести различными способами. Рассмотрим различные способы задания скалярного произведения в двух линейных пространствах 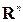и .

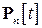Рассмотрим линейное пространство 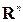. Его элементами являются вектор-столбцы . Скалярное произведение в нем можно задать двумя способами.

Первый способ (задание скалярного произведения стандартным образом):

.

Покажем, что при таком задании скалярного произведения в 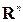выполняются аксиомы 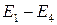евклидова пространства. Действительно, при всех 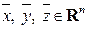, 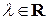имеем:

,

,

,

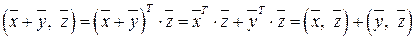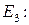
, причем .

Второй способ (задание скалярного произведения в виде симметрической билинейной формы):

,

где симметрическая (, 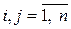) положительно определенная матрица -го порядка.

Замечание 3.1. Доказательство того факта, что скалярное произведение, заданное в виде симметрической билинейной формы, удовлетворяет всем аксиомам евклидова пространства, можно посмотреть в п. 6.7.

Замечание 3.2. Так и являются подпространствами евклидова пространства 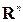, то скалярное произведение в них можно ввести двумя выше описанными способами.

Рассмотрим линейное пространство 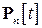. Его элементами являются многочлены относительно переменной степеней, не превосходящих натуральное число :

, .

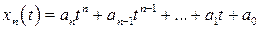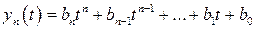Первый способ задания скалярного произведения:

.

Второй способ задания скалярного произведения:

где попарно различные действительные числа.

Можно показать, что в каждом случае выполняются все аксиомы евклидова пространства.

Date: 2015-09-03; view: 696; Нарушение авторских прав