Примеры линейных пространств

Приведем примеры часто встречающихся линейных пространств. Остановимся на так называемых арифметических линейных пространствах.

1) Пространство матриц размера с вещественными элементами:

.

Операции сложения двух матриц и умножения матрицы на число вводятся по законам матричной алгебры:

,

причем эти операции не выводят элементы за пределы множества . Нулевым элементом в является нулевая матрица

,

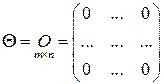а противоположным элементом к матрице является матрица .

Непосредственно можно показать, что для множества выполняются все аксиомы линейного пространства. Действительно, в этом случае аксиомы 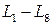линейного пространства соответствуют свойствам операций над матрицами.

2) Пространство вектор-столбцов размера с вещественными элементами (частный случай пространства ):

.

(заметим, что в обозначении вектора 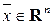наверху присутствует черта, так мы будем обозначать вектор-столбцы). Операции сложения двух вектор-столбцов и умножения вектор-столбца 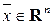на число 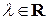вводятся покомпонентно:

, .

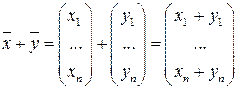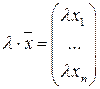Нулевым элементом в является нулевой вектор-столбец

.

Линейное пространство называют линейным арифметическим пространством. Сами элементы (вектор-столбцы) пространства называются арифметическими -мерными вектор-столбцами.

Замечание. Нередко в линейной алгебре можно встретить обозначение пространства в виде

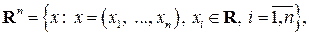
элементами которого являются упорядоченные совокупности действительных чисел. Операции над элементами этого множества вводятся покомпонентно

.

3) Пространство 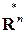вектор-строк размера с вещественными элементами:

.

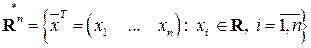Элементами этого пространства являются арифметические -мерные вектор-строки (арифметические вектор-строки помимо черточек будем снабжать верхним индексом 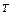, указывающим на транспонирование). Операции в пространстве 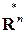определяются также как в пространстве .

4) Пространство многочленов относительно переменной 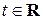с вещественными коэффициентами степеней, не превышающих число :

.

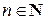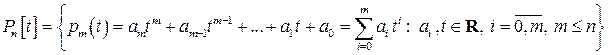Операции сложения двух многочленов и умножения многочлена на действительное число производятся следующим образом:

,

.

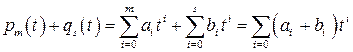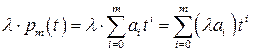Нулевым элементом в является многочлен с нулевыми коэффициентами

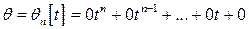
5) Рассмотрим однородную систему линейных алгебраических уравнений (далее ОСЛАУ)

с основной матрицей размера 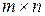. Решениями ОСЛАУ являются вектор-столбцы .

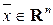Из свойств решений ОСЛАУ известно, что вектор-столбец, полученный в результате суммы двух решений 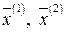или умножения решения на действительное число снова будет являться решением ОСЛАУ. Можно непосредственно проверить, что все аксиомы линейного пространства в этом случае выполняются. Нулевым вектором, естественно, необходимо считать тривиальное решение 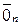ОСЛАУ.

Полученное множество всех решений ОСЛАУ называется линейным пространством решений однородной системы линейных алгебраических уравнений (оно же называется нуль-пространством матрицы ) и обозначается в виде:

.

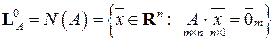Введем дополнительные определения.

Определение 1.2. Конечной системой векторов в линейном пространстве называется конечная совокупность

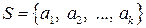
векторов ().

Определение 1.3. Вектор 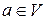называется линейной комбинацией векторов из системы 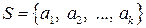(, ), если

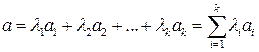, (1.1)

где действительные числа (называемые весовыми коэффициентами, или просто, коэффициентами линейной комбинации).

6) Рассмотрим множество

,

которое назовем множеством, порожденным системой вектор-столбцов 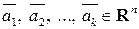. На этом множестве операции сложения векторов и умножения вектора на число введем, как в пространстве . При этом множество будет замкнуто относительно введенных операций. Действительно, если 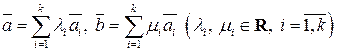, то

,

.

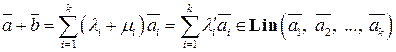Можно доказать, что все аксиомы линейного пространства выполняются для множества . В частности, нулевым элементом является нулевой вектор-столбец

.

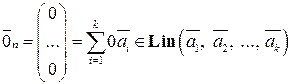Линейное пространство называется пространством, порожденным системой вектор-столбцов .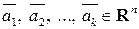

Date: 2015-09-03; view: 444; Нарушение авторских прав