Построение базисов в линейных пространствах

В этом пункте укажем базисы и размерности наиболее часто встречающихся линейных пространств, введенных в пункте 1.2. Для каждого конечномерного линейного пространства обычно определяют так называемый элементарный (стандартный) базис 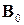(наиболее простой и удобный при решении задач). Также дадим критерии проверки того, при каком условии заданная система векторов является базисом линейного пространства.

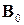1) Линейное пространство . Элементарным базисом в является упорядоченная система -мерных вектор-столбцов

, ,

где все компоненты вектор-столбца 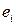(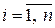) равны нулю, кроме одной, которая равна единице и располагается в позиции, указываемой номером в его обозначении. Таким образом, .

Нетрудно доказать, что упорядоченная система -мерных вектор-столбцов

, (1.11)

где (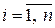), является базисом пространства тогда и только тогда, когда квадратная -матрица

,

столбцами которой являются векторы 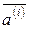(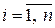), является неособенной матрицей.

При этом если задан вектор-столбец 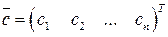, то для нахождения координатного вектор-столбца 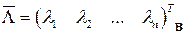в базисе (1.11) достаточно решить систему линейных алгебраических уравнений

,

которая в силу неособенности матрицы , имеет единственное решение.

2) Линейное пространство . Элементарным базисом в является упорядоченная система матриц

,

где все элементы матрицы 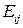(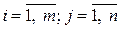) равны нулю, кроме одного, который равен единице и располагается в позиции, указываемой двумя номерами в обозначении. Таким образом, .

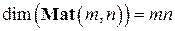Нетрудно доказать, что упорядоченная система матриц

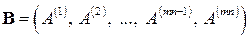, (1.12)

где 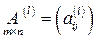(), является базисом в тогда и только тогда, когда матрица

,

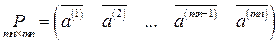столбцами которой являются вектор-столбцы

(),

является неособенной квадратной матрицей.

При этом если задана матрица (), то для нахождения координатного вектор-столбца этой матрицы в базисе (1.12) достаточно решить систему линейных алгебраических уравнений

,

где , которая в силу неособенности матрицы , имеет единственное решение.

3) Линейное пространство . Известно (см. п. 1.2), что если , то система уравнений

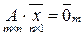
имеет ровно линейно независимых решений, образующих фундаментальную систему решений (ФСР):

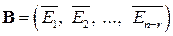, (1.13)

где .

При этом любое решение можно выразить в виде

,

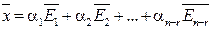где коэффициенты 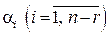определяются однозначно. При этом координатный вектор-столбец вектора имеет вид 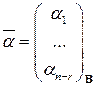. Таким образом, система (1.13) является базисом в пространстве 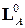и .

Пример 1.2. Найти базис и размерность пространства 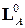решений системы

Решение. Приводим матрицу системы к ступенчатому виду

.

Ранг матрицы . Принимая переменные 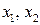за базисные, а за свободные (обозначаем при этом 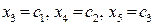), получим общее решение рассматриваемой ОСЛАУ

Составляем базис 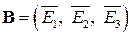пространства решений 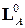(фундаментальную систему решений, при этом ):

.

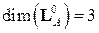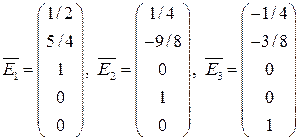4) Рассмотрим алгоритм построения базиса в пространстве , порожденным системой вектор-столбцов .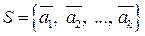

Составим матрицу 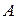размера , столбцами которой являются векторы 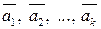. Приведем ее к ступенчатому виду 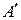с помощью элементарных преобразований над строками (можно допустить и перестановку местами столбцов, если при этом запоминать номера (индексы) столбцов). Столбцы ступенчатой матрицы 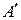, соответствующие столбцам ее базисного минора, определяют порождающие базисные вектор-столбцы в .

Ранг определяет ранг системы векторов (максимальное количество линейно независимых векторов системы).

Соберем базисные векторы в матрицу размера :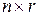

,

где – базис пространства (максимальная порождающая система линейно независимых векторов). При этом имеем

.

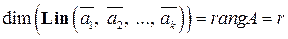Если требуется найти координатный вектор-столбец вектора в базисе 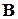, то необходимо решить систему

,

которая имеет единственное решение относительно .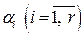

В частности, для определения координатных вектор-столбцов в базисе векторов 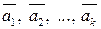необходимо решить систему

,

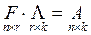где 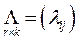– матрица, столбцами которой являются соответствующие координатные вектор-столбцы векторов .

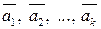Пример 1.3. Найти базис и размерность пространства , где

Найти координатные вектор-столбцы векторов в найденном базисе.

Решение. Составим матрицу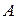

,

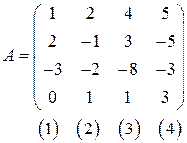столбцами которой являются векторы (под столбцами матрицы расставлены номера соответствующих вектор-столбцов). Приведем ее к ступенчатому виду 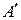с помощью элементарных преобразований (нумерация столбцов не изменилась)

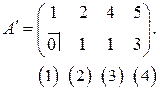
Тогда , векторы – порождающие базисные вектор-столбцы в 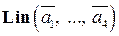(они соответствуют столбцам базисного минора матрицы 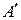). Итак, базис , размерность .

Для нахождения координатного вектор-столбца 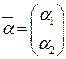вектора 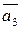в базисе решим соответствующую систему

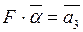
с матрицей .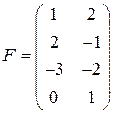

Получим , то есть .

Аналогично найдем координатный вектор-столбец 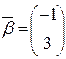вектора базисе . При этом .

Date: 2015-09-03; view: 639; Нарушение авторских прав