Классификация линий и поверхностей 2-го порядка

17.1. Сформулируем важную теорему, позволяющую нам классифицировать линии и поверхности 2-го порядка.

Теорема. В евклидовом пространстве для любой квадратичной формы существуетортонормированный базис, в котором эта форма имеет канонический вид.

Эту теорему мы примем без доказательства.

Мы будем рассматривать обычное двумерное (или трехмерное) пространство с привычным для нас скалярным умножением геометрических векторов. Теорема утверждает, что любая квадратичная форма на плоскости (или в пространстве) приводится к каноническому виду, причем канонический базис является ортонормированным: базисные векторы взаимно перпендикулярны и имеют единичную длину.

17.2. Линии 2-го порядка. Произвольная линия 2-го порядка на плоскости задается уравнением вида . (*)

Первые три слагаемых в левой части уравнения задают квадратичную форму

.

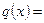
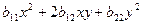Согласно теореме существует ортонормированный базис плоскости, в котором форма 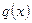принимает канонический вид: .

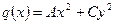В этом базисе уравнение линии будет выглядеть следующим образом:

.

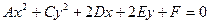Теперь рассмотрим различные случаи.

1 случай. , т.е. коэффициенты и 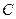одного знака. Будем считать, что и 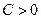(в противном случае умножим все уравнение на -1). Выделением полных квадратов легко привести уравнение к виду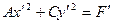

(это соответствует сдвигу начала координат).

А). При уравнение можно записать в виде 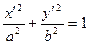. Это уравнение эллипса.

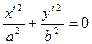Б). При получаем . Это пара мнимых пересекающихся прямых 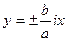. На плоскости есть только единственная точка, удовлетворяющая этому уравнению – точка .

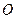В). При 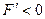получаем . Это мнимый эллипс. На плоскости нет точек, удовлетворяющих уравнению.

2 случай. , т.е. коэффициенты и 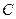разных знаков. Будем считать, что , . Опять выделяем полные квадраты и получаем .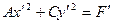

А). При уравнение можно записать в виде 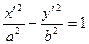. Это уравнение гиперболы. Стоит отметить, что асимптотами гиперболы являются прямые 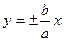. Случай аналогичен: поменяв базисные векторы, получим снова то же уравнение.

Б). При уравнение примет вид 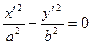. Это пара пересекающихся прямых .

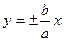3 случай. . Будем считать, что . Заметим, что . Выделим полный квадрат из слагаемых, содержащих 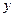. Получим .

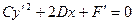А). Если 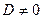, то преобразуем уравнение так: , .

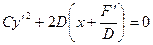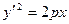Это уравнение параболы.

Б). Если , то уравнение принимает вид .

Если 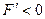, то уравнение можно записать в виде . Это пара параллельных прямых .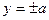

Если , то имеем 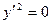- пара совпадающих прямых .

Если , то уравнение можно записать в виде . Это пара мнимых параллельных прямых .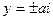

Итак, возможны 9 различных вариантов линий 2-го порядка, в двух из которых множество точек плоскости пусто.

17.3. Классификация поверхностей второго порядка. Уравнение поверхности 2-го порядка имеет вид:

.

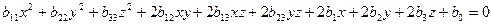Свяжем с этим уравнением квадратичную форму

.

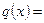
Согласно теореме существует ортонормированный базис, в котором квадратичная форма имеет канонический вид. В этом базисе уравнение поверхности запишется так:

.

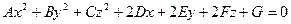Рассмотрим различные случаи.

1 случай. Ранг квадратичной формы равен 3, т.е. коэффициенты 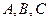не равны нулю. Выделяя полные квадраты, приведем уравнение к виду: .

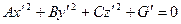А). .

А1). . Уравнение принимает вид . Это уравнение эллипсоида. Любые сечения этой поверхности плоскостями, параллельными координатным плоскостям, являются эллипсами.

А2). 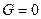. Уравнение принимает вид . Этому уравнению удовлетворяет единственная точка пространства - точка .

А3). 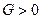. Мы получаем уравнение так называемого мнимого эллипса 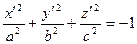. Множество точек, ему удовлетворяющих, пусто.

Б). .

Б1). . Уравнение принимает вид . Это однополостный гиперболоид. Его горизонтальные сечения являются эллипсами, а сечения координатными плоскостям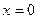и и 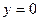- гиперболы.

Б2). 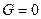. Уравнение приводится к виду 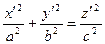и задает конус.

Б3). 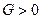. В этом случае получим 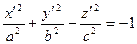, соответствующей поверхностью является двуполостный гиперболоид.

В). Случай 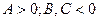сводится к случаю Б) перестановкой базисных векторов.

Г). Случай полностью аналогичен случаю А). Следует только умножить все уравнение на -1.

2 случай. Ранг квадратичной формы равен 2, т.е. один из коэффициентов 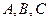равен нулю. Будем считать, что 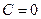. После выделения полных квадратов получим уравнение вида .

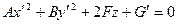А). Если 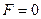, то окажется, что уравнение не содержит переменной 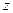. Это означает, что поверхность является цилиндром.

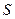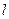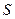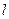Определение. Поверхность называется цилиндром, параллельным прямой , если из того, что точка принадлежит , следует, что все точки прямой, проходящей через точку и параллельной , принадлежат поверхности .

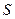Горизонтальным сечением такого цилиндра может быть эллипс, гипербола, пара пересекающихся прямых, точка или пустое множество в зависимости от того, какую линию на плоскости задает уравнение .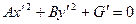

Б). Пусть .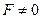

Б1). Если 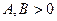, то уравнение приводится к виду . Это уравнение эллиптического параболоида.

Б2). Если 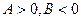, то уравнение приводится к виду 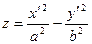. Это уравнение задает гиперболический параболоид. Его горизонтальные сечения – гиперболы. Сечение плоскостью 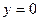является параболой, ветви которой направлены вверх, а сечение плоскостью 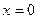является параболой, ветви которой направлены вниз.

3 случай. Ранг квадратичной формы равен 1. В этом случае уравнение имеет вид

.

Выделив полный квадрат из первых двух слагаемых, придем к уравнению

.

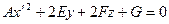А). Пусть 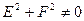. Сделаем замену координат:

, .

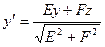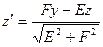Заметьте – матрица перехода ортогональна, базис остался ортонормированным. В этом базисе уравнение выглядит так: .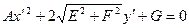

Из этого уравнения легко получить .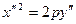

Мы получили уравнение параболического цилиндра.

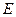Б). Пусть теперь , т.е. коэффициенты и 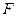равны нулю. Тогда от уравнения останется .

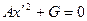Б1). При условии 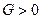уравнение можно записать в виде 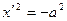, и мы получим пару мнимых параллельных плоскостей .

Б2). При условии 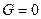уравнение превращается в уравнение и задает пару совпадающих плоскостей .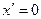

Б3). При условии уравнение можно записать в виде 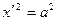, и мы получим пару параллельных плоскостей .

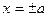Date: 2015-09-03; view: 641; Нарушение авторских прав