
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

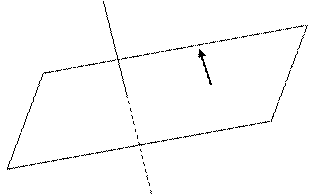
Плоскость в пространстве
|
|
11.1 Общее уравнение плоскости. Зафиксируем декартову прямоугольную систему координат. Рассмотрим произвольное уравнение первой степени
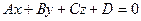 . (*)
. (*)
Заметим, что хотя бы один из коэффициентов 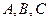 не равен нулю (иначе это уравнение имело бы нулевую степень). Тогда уравнение (*) имеет хотя бы одно решение
не равен нулю (иначе это уравнение имело бы нулевую степень). Тогда уравнение (*) имеет хотя бы одно решение  , т.е. существует хотя бы одна точка, координаты которой удовлетворяют уравнению (*):
, т.е. существует хотя бы одна точка, координаты которой удовлетворяют уравнению (*): 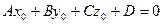 . (**)
. (**)
Вычтем из уравнения (*) уравнение (**): 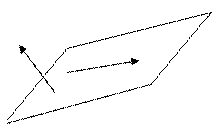
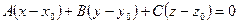 . (***)
. (***)
Уравнение (***) эквивалентно уравнению (*), т.е. если координаты точки удовлетворяют уравнению (*), то они удовлетворяют уравнению (***), и наоборот.
Обозначим  вектор с координатами
вектор с координатами 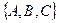 . Пусть
. Пусть 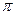 - плоскость, проходящая через точку
- плоскость, проходящая через точку  и перпендикулярная вектору
и перпендикулярная вектору  . Если точка
. Если точка 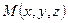 лежит в плоскости
лежит в плоскости 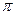 , то вектор
, то вектор  перпендикулярен вектору
перпендикулярен вектору  , скалярное произведение этих векторов равно 0. Тогда координаты точки
, скалярное произведение этих векторов равно 0. Тогда координаты точки  удовлетворяют уравнению (***) и, следовательно, уравнению (*). Если же точка
удовлетворяют уравнению (***) и, следовательно, уравнению (*). Если же точка 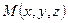 не лежит в плоскости
не лежит в плоскости 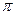 , то векторы
, то векторы  и
и  не перпендикулярны, и скалярное произведение этих векторов не равно 0. Значит, в этом случае координаты точки
не перпендикулярны, и скалярное произведение этих векторов не равно 0. Значит, в этом случае координаты точки  не удовлетворяют уравнению (***) и уравнению (*).
не удовлетворяют уравнению (***) и уравнению (*).
Пусть теперь дана произвольная плоскость. Выберем вектор  , перпендикулярный этой плоскости, и произвольную точку
, перпендикулярный этой плоскости, и произвольную точку  , лежащую в этой плоскости. Если
, лежащую в этой плоскости. Если 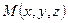 произвольная точка плоскости, то векторы
произвольная точка плоскости, то векторы  и
и  перпендикулярны, их скалярное произведение равно 0. Тогда координаты точки удовлетворяют уравнению (***) и, следовательно, уравнению (*), являющимся уравнением первой степени. Мы доказали
перпендикулярны, их скалярное произведение равно 0. Тогда координаты точки удовлетворяют уравнению (***) и, следовательно, уравнению (*), являющимся уравнением первой степени. Мы доказали
Утверждение. Произвольная плоскость в пространстве определяется уравнением первой степени. Обратно, любое уравнение первой степени определяет в пространстве плоскость.
Уравнение (*) называется общим уравнением плоскости.
11.2. Нормированное уравнение плоскости. Заметим, что коэффициенты уравнения (*) определены с точностью до пропорциональности. Умножив все коэффициенты на одно и то же не равное нулю число, мы получим новое уравнение, но оно будет задавать ту же плоскость. Если потребовать, чтобы вектор нормали  , который до сих пор был произвольным, имел единичную длину, т.е.
, который до сих пор был произвольным, имел единичную длину, т.е. 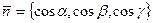 , то он будет определен однозначно (с точностью до знака). Запишем теперь уравнение плоскости в таком виде:
, то он будет определен однозначно (с точностью до знака). Запишем теперь уравнение плоскости в таком виде: 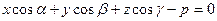 . Этот вид уравнения называют нормированным.
. Этот вид уравнения называют нормированным.
Выясним геометрический смысл коэффициента 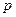 . Если точка
. Если точка 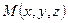 лежит в плоскости
лежит в плоскости 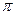 , то из равенства
, то из равенства 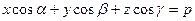
 следует, что
следует, что 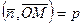 . Так как вектор
. Так как вектор  имеет единичную длину, то
имеет единичную длину, то 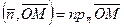 .
.
Значит, 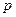 - это проекция любого радиус-вектора точки, лежащей на плоскости.
- это проекция любого радиус-вектора точки, лежащей на плоскости.
11.3. Уравнение плоскости в отрезках. Общее уравнение плоскости (*) называется полным, если все коэффициенты 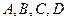 отличны от нуля. В противном случае оно называется неполным. Неполные уравнения задают плоскость, проходящую через начало координат, параллельную какой-либо координатной оси или параллельную какой-либо координатной плоскости. Все эти случаи несложно рассмотреть.
отличны от нуля. В противном случае оно называется неполным. Неполные уравнения задают плоскость, проходящую через начало координат, параллельную какой-либо координатной оси или параллельную какой-либо координатной плоскости. Все эти случаи несложно рассмотреть.
 Мы же рассмотрим полное уравнение плоскости. Так как все коэффициенты общего уравнения отличны от нуля, его можно переписать в виде:
Мы же рассмотрим полное уравнение плоскости. Так как все коэффициенты общего уравнения отличны от нуля, его можно переписать в виде: 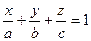 ,
,
где 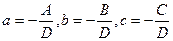 . Этот вид уравнения плоскости называется уравнением плоскости в отрезках. Коэффициенты
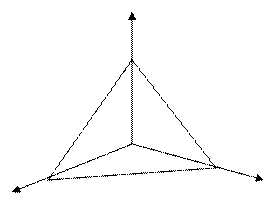
. Этот вид уравнения плоскости называется уравнением плоскости в отрезках. Коэффициенты 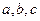 имеют прозрачный геометрический смысл: это длины отрезков, которые плоскость отсекает на координатных осях. Чтобы увидеть это, надо найти точки пересечения плоскости с координатными осями. Например, чтобы найти точку пересечения плоскости с осью
имеют прозрачный геометрический смысл: это длины отрезков, которые плоскость отсекает на координатных осях. Чтобы увидеть это, надо найти точки пересечения плоскости с координатными осями. Например, чтобы найти точку пересечения плоскости с осью 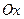 , надо в уравнении плоскости в отрезках положить
, надо в уравнении плоскости в отрезках положить 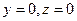 . Мы сразу же получим
. Мы сразу же получим  . Остальные точки пересечения находятся аналогично.
. Остальные точки пересечения находятся аналогично.
11.4. Уравнение плоскости, проходящей через три заданные точки.
Поставим задачу: написать уравнение плоскости, проходящей через три данные точки, не лежащие на одной прямой. Пусть эти точки заданы своими координатами:  ,
,  ,
, 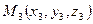 . Так как эти точки не лежат на одной прямой, то векторы
. Так как эти точки не лежат на одной прямой, то векторы  и
и 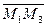 не коллинеарны. Тогда точка
не коллинеарны. Тогда точка 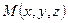 принадлежит той же плоскости, что и точки
принадлежит той же плоскости, что и точки 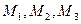 , тогда и только тогда, когда векторы
, тогда и только тогда, когда векторы  ,
, 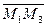 ,
, 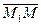 компланарны. Это условие равносильно равенству нулю смешанного произведения этих векторов:
компланарны. Это условие равносильно равенству нулю смешанного произведения этих векторов:

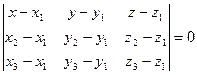 .
.
Это уравнение является уравнением первой степени и дает нам искомое уравнение плоскости.
11.5. Угол между плоскостями. Пусть заданы две плоскости своими общими уравнениями: 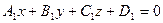 ,
,  .
.
Очевидно, что вопрос о нахождении угла между плоскостями сводится к нахождению угла между их нормалями:
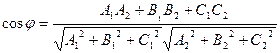 .
.
Условие параллельности двух плоскостей сводится к вопросу о коллинеарности векторов нормали: плоскости параллельны тогда и только тогда, когда координаты векторов нормали пропорциональны.
Две плоскости перпендикулярны тогда и только тогда, когда перпендикулярны их нормали, т.е. скалярное произведение векторов нормали равно нулю:
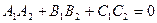 .
.
 12. Прямая в пространстве.
12. Прямая в пространстве.
12.1 Канонические уравнения прямой в пространстве. Договоримся называть любой ненулевой вектор, параллельный данной прямой, направляющим вектором этой прямой. Выведем уравнение прямой, проходящей через данную точку  и параллельную данному направляющему вектору
и параллельную данному направляющему вектору 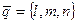 . Заметим, что точка
. Заметим, что точка 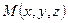 лежит на этой прямой тогда и только тогда, когда векторы
лежит на этой прямой тогда и только тогда, когда векторы  и
и 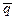 коллинеарны. Это означает, что координаты этих векторов пропорциональны:
коллинеарны. Это означает, что координаты этих векторов пропорциональны: 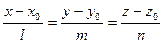 .
.
Эти уравнения называют каноническими. Заметим, что одна или две координаты направляющего вектора могут оказаться равными нулю. Но мы воспринимаем это как пропорцию: 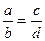 мы понимаем как равенство
мы понимаем как равенство 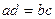 .
.
12.2. Параметрические уравнения прямой в пространстве. Откладывая от точки  векторы
векторы 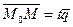 для различных значений
для различных значений 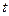 , коллинеарные направляющему вектору, мы будем получать на конце отложенных векторов различные точки нашей прямой. Из равенства
, коллинеарные направляющему вектору, мы будем получать на конце отложенных векторов различные точки нашей прямой. Из равенства 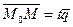 следует:
следует:
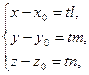 или
или 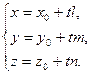
Переменную величину 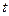 называют параметром. Поскольку для любой точки прямой найдется соответствующее значение параметра и поскольку различным значениям параметра соответствуют различные точки прямой, то существует взаимно однозначное соответствие между значениями параметра и точками прямой. Когда параметр
называют параметром. Поскольку для любой точки прямой найдется соответствующее значение параметра и поскольку различным значениям параметра соответствуют различные точки прямой, то существует взаимно однозначное соответствие между значениями параметра и точками прямой. Когда параметр 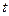 пробегает все действительные числа от
пробегает все действительные числа от 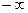 до
до 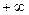 , соответствующая точка
, соответствующая точка 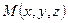 пробегает всю прямую.
пробегает всю прямую.
Очевидна механическая интерпретация параметрических уравнений. Если считать, что 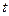 - это время,
- это время,  - начальное положение точки при
- начальное положение точки при  , вектор
, вектор 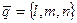 - постоянный вектор скорости, то параметрические уравнения описывают закон равномерного движения точки.
- постоянный вектор скорости, то параметрические уравнения описывают закон равномерного движения точки.
Параметрические уравнение легко получаются из канонических уравнений: достаточно лишь приравнять три отношения, участвующие в канонических уравнениях, к параметру 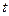 .
.
12.3. Уравнения прямой, проходящей через две данные точки. Пусть даны две точки  и
и  . Чтобы найти канонические уравнения прямой, проходящей через эти точки, заметим, что вектор
. Чтобы найти канонические уравнения прямой, проходящей через эти точки, заметим, что вектор  является направляющим вектором этой прямой. Тогда искомые уравнения имеют вид:
является направляющим вектором этой прямой. Тогда искомые уравнения имеют вид:
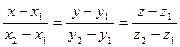 .
.
12.4. Угол между двумя прямыми. Задача нахождения угла между двумя прямыми сводится к нахождению угла между их направляющими векторами. Если прямые заданы своими каноническими уравнениями
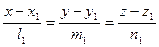 и
и 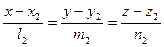 ,
,
то векторы 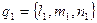 и
и 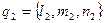 являются их направляющими векторами. Тогда косинус угла между прямыми можно найти, используя скалярное произведение:
являются их направляющими векторами. Тогда косинус угла между прямыми можно найти, используя скалярное произведение:
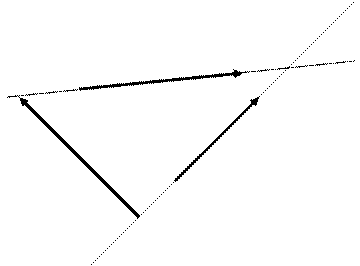
 .
.
Прямые параллельны, если коллинеарны их направляющие векторы:
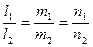 .
.
Прямые перпендикулярны, если перпендикулярны их направляющие векторы, т.е. их скалярное произведение равно нулю:  .
.
12.5. Взаимное расположение двух прямых в пространстве. В пространстве взаимное расположение двух прямых может быть следующим: 1) эти прямые параллельны (в частности, совпадают), 2) они пересекаются, 3) они скрещиваются. В первых двух случаях прямые лежат в одной плоскости. Найдем, когда две прямые принадлежат одной плоскости. Пусть эти прямые заданы своими каноническими уравнениями 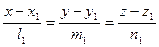 и
и 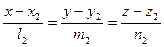 , Рассмотрим три вектора:
, Рассмотрим три вектора:  ,
,  и
и  . Для того, чтобы прямые принадлежали одной плоскости, необходимо и достаточно, чтобы эти векторы были компланарны. Это выполняется тогда и только тогда, когда смешанное произведение этих трех векторов равно нулю, т.е.
. Для того, чтобы прямые принадлежали одной плоскости, необходимо и достаточно, чтобы эти векторы были компланарны. Это выполняется тогда и только тогда, когда смешанное произведение этих трех векторов равно нулю, т.е.
 .
.
Если при этом координаты направляющих векторов пропорциональны, то эти прямые параллельны.
12.6. Взаимное расположение прямой и плоскости. Пусть нам заданы прямая
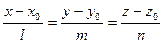
и плоскость 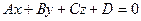 . Так как угол
. Так как угол 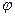 между прямой и плоскостью и угол
между прямой и плоскостью и угол 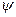 между прямой и нормальным вектором к плоскости связаны очевидным равенством
между прямой и нормальным вектором к плоскости связаны очевидным равенством 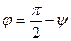 , то
, то 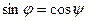 . Поэтому
. Поэтому 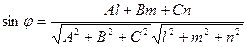 .
.
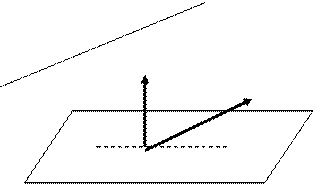 Условие перпендикулярности прямой и плоскости соответствует коллинеарности направляющего вектора прямой и нормали к плоскости.
Условие перпендикулярности прямой и плоскости соответствует коллинеарности направляющего вектора прямой и нормали к плоскости.
Условие параллельности прямой и плоскости – или перпендикулярности прямой и нормального вектора к плоскости - можно записать в виде  . Частный случай параллельности – прямая принадлежит плоскости – выполняется, если еще и какая-нибудь точка прямой принадлежит плоскости, например, выполняется равенство
. Частный случай параллельности – прямая принадлежит плоскости – выполняется, если еще и какая-нибудь точка прямой принадлежит плоскости, например, выполняется равенство  .
.
12.7. Расстояние от точки до плоскости. Пусть нам заданы точка  и плоскость
и плоскость 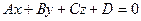 . Проведем через точку
. Проведем через точку  прямую, перпендикулярную плоскости. Заметим, что вектор нормали к плоскости может служить направляющим вектором этой прямой:
прямую, перпендикулярную плоскости. Заметим, что вектор нормали к плоскости может служить направляющим вектором этой прямой: 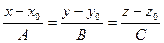 .
.
Перейдем к параметрическим уравнениям:
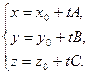
Найдем, при каком значении параметра точка прямой будет принадлежать плоскости. Для этого подставим параметрические уравнения прямой в уравнение плоскости и решим получившееся уравнение относительно 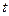 :
:
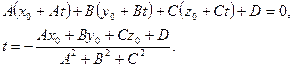
Расстояние от точки  до точки, соответствующей этому значению параметра, равно длине вектора
до точки, соответствующей этому значению параметра, равно длине вектора 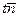 . Нам осталось найти эту длину:
. Нам осталось найти эту длину:

Это и есть расстояние от точки  до плоскости.
до плоскости.
Date: 2015-09-03; view: 500; Нарушение авторских прав