Билинейные и квадратичные формы

15.1. Основные понятия. Пусть - конечномерное линейное пространство, .

Определение. Билинейной формой (билинейной функцией) называется функция двух аргументов , линейная по каждому аргументу, т.е. для всех R выполняются равенства

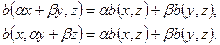
Из определения билинейной формы сразу же следует, что .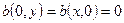

Пример. Если - пространство геометрических векторов, то скалярное произведение является билинейной формой.

Зафиксируем в пространстве базис . В этом базисе векторы и 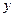имеют разложения , 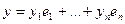. Тогда:

, где .

Матрицу 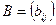называют матрицей билинейной формы в базисе 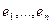. Если , , 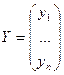то матричная запись значений билинейной формы выглядит следующим образом: .

Обратно, имея произвольную квадратную матрицу, можно построить соответствующую билинейную форму.

15.2. Изменение матрицы билинейной формы при замене базиса. Пусть 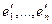- другой базис пространства, 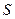- матрица перехода от 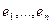к 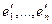. Тогда ( - координаты векторов 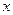и 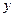в новом базисе). Имеем:

. Значит, .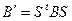

Date: 2015-09-03; view: 371; Нарушение авторских прав