Канонический вид квадратичной формы

Определение. Базис 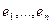пространства будем называть каноническим для квадратичной формы 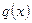, если матрица квадратичной формы диагональна, т.е.

.

Говорят, что квадратичная форма приводится к каноническому виду, если для нее существует канонический базис.

Теорема. Для любой квадратичной формы существует канонический базис.

Доказательство проведем методом Лагранжа. Пусть

-

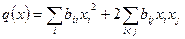квадратичная форма. Пусть не все коэффициенты 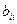равны нулю. Без ограничения общности считаем, что 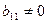. Соберем все слагаемые, содержащие :

.

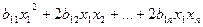Выделим полный квадрат: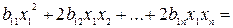

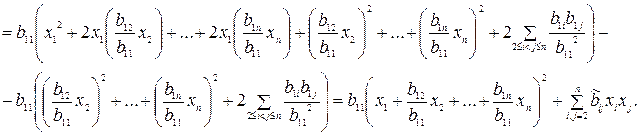
Теперь форму 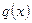можно представить в ви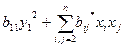де

, где .

Переход к новому базису, соответствующий замене координат

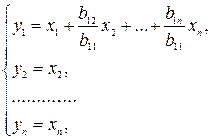
осуществляется при помощи невырожденной матрицы перехода.

Далее продолжаем действовать аналогично: выбираем координату, коэффициент при квадрате которой отличен от нуля, собираем все слагаемые, содержащие эту координату, выделяем полный квадрат и т.д. За конечное число шагов мы получим канонический вид квадратичной формы.

Проблемы могут возникнуть, если на каком-то этапе не найдется координаты, коэффициент при квадрате которой отличен от нуля. Возможны два варианта. Если ненулевых коэффициентов нет совсем, то процесс закончен – форма приобрела канонический вид (с 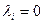для некоторых ). Если же найдется коэффициент 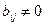для некоторых 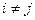, то сделаем такое (невырожденное) преобразование:

Появятся (несократимые) слагаемые 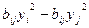. Теорема доказана.

15.6. Закон инерции. Итак, для любой квадратичной формы существует базис, в котором форма имеет вид: .

Если потребовать, чтобы коэффициенты 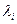были положительными, то канонический вид формы будет таким: .

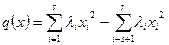Число 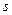- количество положительных коэффициентов - называется положительным индексом формы, число - количество отрицательных коэффициентов - называется отрицательным индексом формы, число 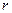- рангом квадратичной формы.

Заметим, что выбор канонического базиса неоднозначен. Поэтому возникает естественный вопрос: зависит ли положительный или отрицательный индекс формы от выбора базиса? Ответ дает следующая теорема.

Теорема (закон инерции). Положительный и отрицательный индексы формы не зависят от выбора базиса.

Доказательство. Пусть в каноническом базисе 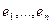квадратичная форма имеет вид 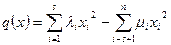, причем 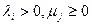. Пусть в другом каноническом базисе 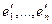квадратичная форма имеет другой вид , .

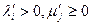Докажем независимость от базиса положительного индекса формы. Предположим, что , например, 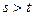. Рассмотрим множество векторов 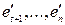. Этих векторов в сумме больше, чем 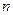, поэтому они линейно зависимы. Существует нетривиальная линейная комбинация этих векторов, равная нулю:

, .

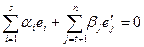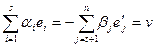Заметим, что вектор не может быть нулевым, поскольку векторы 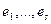линейно независимы и векторы 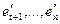линейно независимы.

Однако, .

С другой стороны, .

Мы получили противоречие. Значит, .

Аналогично можно получить, что отрицательный индекс не зависит от выбора базиса. Теорема доказана.

Если в каноническом виде квадратичной формы все коэффициенты положительны, то для любого ненулевого вектора 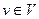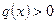. Такая форма называется положительно определенной. Отрицательно определенной называют форму, значения которой на каждом ненулевом векторе пространства отрицательны. Возникает вопрос, как определить знакоопределенность формы, не приводя ее к каноническому базису.

15.7. Критерий Сильвестра. Зафиксируем в пространстве некоторый базис 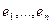. В этом базисе квадратичная форма имеет матрицу .

Теорема (критерий Сильвестра). Квадратичная форма 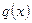является положительно определенной тогда и только тогда, когда все главные миноры ее матрицы больше нуля.

Мы опустим строгое доказательство, приведем лишь некоторые рассуждения.

Если форма положительно определена, то существует базис, в котором ее матрица является единичной. Пусть 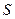- матрица перехода к этому базису. Тогда ,

.

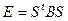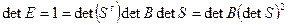Отсюда следует, что определитель матрицы положительно определенной квадратичной формы больше нуля. Но положительности определителя матрицы недостаточно для ее положительной определенности. Так, например, определитель матрицы

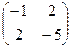
больше нуля, однако, квадратичная форма с такой матрицей 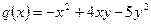не является положительно определенной: на векторе с координатами 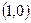ее значение равно -1. Построим цепочку подпространств 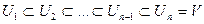, где - это множество векторов, являющихся линейными комбинациями базисных векторов 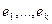. Ограничив квадратичную форму на подпространство , мы получим квадратичную форму на нем с матрицей, совпадающей с матрицей главного минора. Те же соображения, что и для всего пространства, приводят к утверждению о положительности этого минора.

Date: 2015-09-03; view: 575; Нарушение авторских прав