Линейные отображения и операторы

13.1. Преобразование координат вектора при переходе от одного базиса к другому в линейном пространстве. Вернемся к линейным пространствам вообще – произвольным и произвольной (но конечной) размерности. До сих пор мы рассматривали пространства с некоторым фиксированным базисом. В этом базисе каждый вектор имел свои координаты, которые определялись однозначно. Посмотрим, как изменятся координаты вектора, если один базис линейного пространства заменить другим. Итак, пусть в линейном пространстве зафиксирован базис 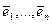. Произвольный вектор 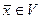имеет некоторое разложение по этому базису: .

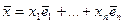Возьмем теперь другой базис 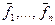. Каждый вектор нового базиса имеет свое разложение по старому базису:

Матрица 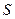, составленная из координат нового базиса в старом базисе, называется матрицей перехода:

.

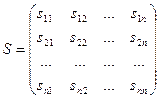Заметим, что –й столбец матрицы перехода – это столбец координат -го вектора нового базиса в старом базисе.

Теорема. Матрица перехода от одного базиса к другому невырождена, т.е. .

Доказательство предложения следует из того, что столбцы этой матрицы линейно независимы, поскольку являются координатами векторов нового базиса в старом базисе.

Пусть в новом базисе вектор имеет другие координаты:

.

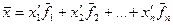Посмотрим, как связаны координаты в новом и старом базисах.

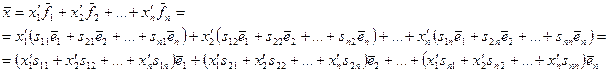
Так как координаты вектора определены однозначно, то:

Эти равенства можно записать в матричном виде:

,

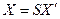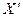или , где - это столбец координат вектора в старом базисе, а - столбец координат этого же вектора в новом базисе. Эту же формулу можно записать в виде , выразив новые координаты вектора через старые.

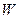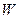13.2. Линейные отображения. Пусть и - два линейных пространства, вообще говоря, различных (но оба пространства должны быть вещественными или оба комплексными). Назовем отображением линейного пространства в пространство закон, по которому каждому вектору из пространства ставится в соответствие единственный вектор из пространства 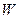. Кратко мы это будем записывать 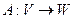. Образ вектора 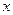при отображении будем обозначать .

Определение. Отображение 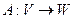называется линейным, если для любых векторов и любых чисел выполняется равенство .

Следует обратить внимание на то, что знак «+» в левой и правой частях равенства обозначает, вообще говоря, разные операции, поскольку и 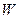- различные пространства. То же самое относится и к операции умножения на число.

Очевидно, что любое линейное отображение переводит нулевой вектор пространства в нулевой вектор пространства .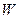

Определение. Если 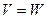, то линейное отображение называют линейным преобразованием, или линейным оператором.

Приведем некоторые примеры линейных отображений.

1). Пусть - линейное пространство и пусть 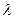- некоторое число (вещественное или комплексное в зависимости от того, каким является пространство ). Поставим каждому вектору 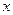из пространства в соответствие вектор . Получившееся отображение является линейным отображением , которое называется гомотетией.

2). Пусть - некоторое линейное пространство размерности 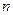. Выберем в нем базис. Сопоставим каждому вектору 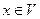столбец его координат. Это соответствие является линейным отображением пространства в арифметическое линейное пространство R ⁿ.

Если же сопоставить каждому вектору его первую координату, то мы получим линейное отображение 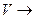R.

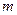3). Зафиксируем матрицу размера х 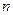. Возьмем арифметическое линейное пространство столбцов R ⁿ. Каждому элементу этого пространства поставим в соответствие столбец . Высота получившегося столбца равна 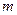. Мы получили линейное отображение из R ⁿ в R ^m.

4). Пусть - линейное пространство многочленов одной переменной 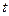. Каждому многочлену поставим в соответствие его производную по переменной 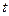. Поскольку производная многочлена является многочленом, мы получим линейное отображение этого пространства на себя.

Пусть 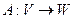- линейное отображение.

Определение. Множество образов всех векторов 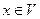называется образом линейного отображения . Обозначение: .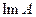

Определение. Множество векторов 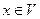, для которых 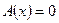, называется ядром отображения . Обозначение: .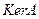

Предложение. Ядро линейного отображения является подпространством в . Образ линейного отображения является подпространством в .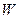

Доказательство. 1). Ядро линейного отображения не пусто: оно всегда содержит нулевой вектор. Если 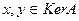, т.е. 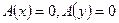, то в силу линейности отображения 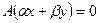для любых чисел .

2). Нулевой вектор пространства 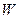принадлежит 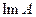, так как является образом нулевого вектора. Далее, если , т.е. существуют векторы 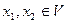такие, ч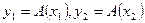то , то .

Предложение доказано.

Задача. В примерах 1)-4) найти ядро и образ каждого отображения.

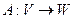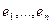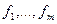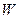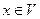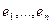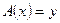13.3. Координатная запись линейных отображений. Пусть - линейное отображение. Зафиксируем базис в пространстве и базис в пространстве . Пусть - произвольный вектор, который в базисе имеет разложение , и пусть его образ имеет в пространстве 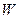разложение . В силу линейности отображения

.

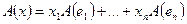Получается, что образ вектора при линейном отображении может быть найден по координатам этого вектора, если известны образы базисных векторов.

Каждый из векторов 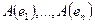может быть разложен по базису :

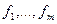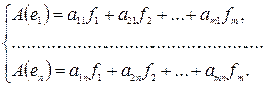
Тогда

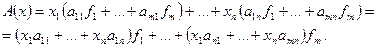
Поскольку координаты вектора определены однозначно, имеем:

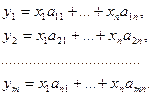
Эти равенства можно записать в матричном виде:

. (*)

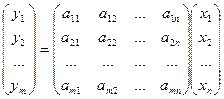Матрицу 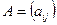размера 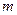х 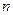назовем матрицей линейного отображения в паре базисов 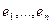и 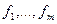. Чтобы различить отображение и его матрицу в некотором базисе, будем отображение обозначать письменной латинской буквой, а его матрицу – печатной: отображение: 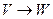, оно имеет матрицу в данном зафиксированном базисе. Образ любого вектора можно найти с помощью этой матрицы, умножив ее слева на столбец координат вектора.

Заметим, что для любой матрицы размера 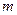х 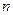существует линейное отображение, такое, что эта матрица является матрицей этого отображения в данной паре базисов.

Рассмотрим отдельно случай, когда линейное отображение является линейным оператором, действующим на 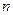-мерном пространстве . Зафиксируем базис в пространстве . Тогда матрица линейного оператора является квадратной и можно говорить об определителе этой матрицы. Заметим, что если 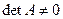, то 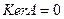. Это следует из того, что система линейных уравнений 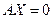имеет единственное нулевое решение. Если же , то эта система имеет ненулевое решение, и в этом случае ядро оператора 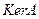нетривиально.

Задача. Пусть - линейное пространство многочленов степени не выше 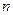. Очевидно, размерность этого пространства равна 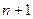. Пусть - линейный оператор , сопоставляющий каждому многочлену его производную. Выберем в качестве базиса одночлены 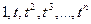. Найдите матрицу оператора в этом базисе.

13.4. Изменение матрицы линейного отображения при замене базисов. Посмотрим, как изменится матрица линейного отображения, если в пространствах и 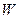перейти к новым базисам. Пусть 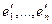и 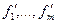- новые базисы. Обозначим через 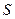матрицу перехода от 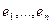к 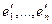, через 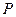- матрицу перехода от 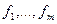к 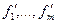. Тогда:

, .

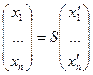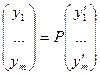Подставим в равенство (*):

.

Отсюда

.

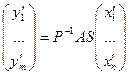Значит, при изменении базисов матрица этого отображения преобразуется в матрицу .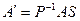

В случае, когда линейное отображение является линейным оператором, вместо пары базисов мы имеем один базис в пространстве . Тогда при замене этого базиса матрица оператора преобразуется по формуле .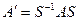

Теорема. Определитель матрицы линейного оператора инвариантен, т.е. не меняется при переходе от одного базиса к другому.

Доказательство. Воспользуемся тем, что определитель произведения матриц равен произведению определителей:

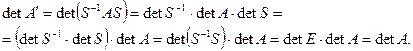
Поскольку определитель матрицы линейного оператора не зависит от базиса, то можно говорить об определителе линейного оператора. Будем называть линейный оператор вырожденным, если его определитель равен нулю, и невырожденным в противном случае.

Date: 2015-09-03; view: 721; Нарушение авторских прав