Линейные многообразия

Подпространствами в V₃ являются только те прямые и плоскости, которые проходят через начало координат. Чтобы включить в круг изучаемых нами объектов любые прямые и плоскости, заметим, что последние получаются из прямых и плоскостей, проходящих через начало координат с помощью сдвига (параллельного переноса). Проведем аналогичное построение в произвольном пространстве.

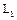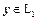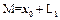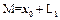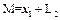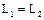Пусть - подпространство в , и . Множество векторов , представимых в виде , где , называется линейным многообразием и обозначается . Линейное многообразие называют также гиперплоскостью или «сдвинутым подпространством». Если и - два представления линейного многообразия , то , а 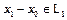. Таким образом многообразие может быть получено сдвигом только одного подпространства.

Размерность линейного многообразия 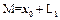(по определению) равна размерности сдвигаемого подпространства, т.е. .

1. Сумма и пересечение подпространств. Пусть - подпространства в . Их пересечение также является подпространством (это утверждение верно для пересечения любого числа подпространств). Объединение подпространств, как правило, не является подпространством. Минимальное подпространство, содержащее 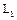и 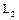, называется их суммой и обозначается 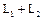. 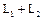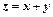Сумма может быть также определена как множество всех , представимых в виде , где 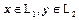. Соотношение между размерностями указанных подпространств устанавливает теорема.

Теорема 1. .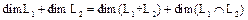

Доказательство. Введем следующие обозначения: , , , .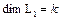

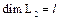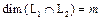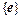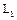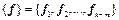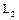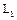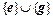Пусть − базис пересечения . Дополним систему до базиса векторами , а до базиса векторами , т.е. − базис , − базис 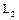. Покажем, что является базисом суммы .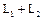

Очевидно, что любой вектор разлагается по системе векторов . Докажем, что эта система линейно независима.

Если система линейно зависима, то некоторая нетривиальная линейная комбинация векторов равна комбинации векторов 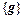. Это значит, что ненулевой вектор 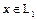разлагается по системе 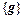, т.е. лежит в подпространстве . Все векторы из разлагаются по базису 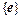и, т.к. система 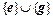линейно независима, не могут быть равны линейной комбинации векторов 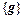. Следовательно, система линейно независима и образует базис 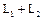. Подсчитав число векторов системы , получим: , т.е. 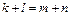, что и требовалось доказать.

Если разложение 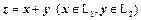однозначно, то сумма подпространств называется прямой и обозначается 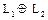. В этом случае размерность суммы подпространств равна сумме их размерностей, а базис суммы можно получить объединением базисов слагаемых.

Также определяется прямая сумма любого числа подпространств.

Date: 2015-09-03; view: 1020; Нарушение авторских прав