Квадратичные формы. Приведите к каноническому виду с помощью ортогонального преобразования

Множество 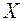является ограниченным, если существует некоторое фиксированное число М такое, что 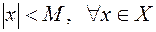. Если такое условие для 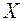не выполнено, то множество называется неограниченным. Множество 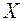называется ограниченным сверху, если существует фиксированное число М такое, что 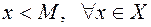. Множество 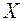называется ограниченным снизу, если существует фиксированное число m такое, что 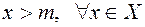. М и m называется верхней и нижней гранью множества. Ограниченное множество является ограниченным сверху и снизу.

Пусть Х - ограниченное сверху множество. Наименьшей из всех верхних граней этого множества называют точной верхней гранью множества Х (супремизм). SupX данного множества. Если Х - ограниченное снизу множество, то наибольшая из нижних граней называется точной нижней гранью (инфимум).

Если множество Х неограничено сверху, то по определению SupX =

Если множество Х неограничено снизу, то по определению.= .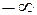

Если точная верхняя грань принадлежит данному множеству, то SupX= maxx. Если infX принадлежит множеству, то infX=minx.

31. Знакоопределенные квадратичные формы. Критерий Сильвестра.

Квадратичная форма называется положительно определенной, если .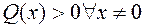

Квадратичная форма называется отрицательно определенной, если .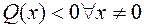

Теорема. Для того, чтобы квадратичная форма 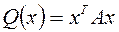, была положительно (отрицательно) определена, необходимо и достаточно, чтобы все собственные значения матрицы А были положительны (отрицательны).

.

Пусть матрица 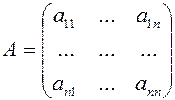. Главными минорами этой матрицы называются миноры .

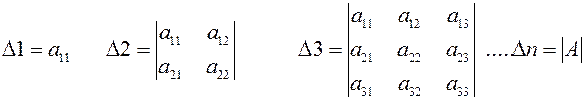Теорема (Критерий Сильвестра).

1) Квадратичная форма положительно определена тогда и только тогда, когда все главные миноры в матрице к-ф положительны.

2) Квадратичная форма отрицательно определена тогда и только тогда, когда знаки главных миноров чередуются следующим образом:

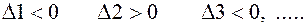
Date: 2015-09-03; view: 1283; Нарушение авторских прав