Базис и размерность линейного пространства. Координаты вектора в базисе и их единственность

Максимальный набор линейно независимых векторов конечномерного пространства называется базисом этого ространства. Нетрудно видеть, что различные базисы данного пространства имеют одинаковое число векторов, это количество векторов в базисе называется размерностью данного пространства.

Теорема: Совокупность линейно независимых векторов линейного пространства 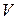является базисом тогда и только тогда, когда для любого вектора x из V является линейной комбинацией векторов.

Доказательство: Пусть - базис и 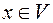докажем, что x- является линейной комбинацией базисных векторов. Рассмотрим набор векторов - данная совокупность векторов линейной зависимости, потому что в ней больше векторов чем в базисе. Значит существуют числа 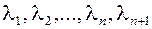не все равные нулю, такие что 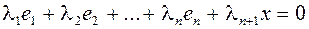. Утверждаем что число 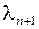не может быть равным нулю. Действуя в противоположном направлении мы получим 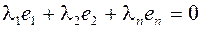, причем существует 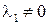из начального набора векторов 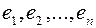- линейно зависимы и поэтому не являются базисом, тогда (Лена, я тебя очень люблю(твой Сергей))

.

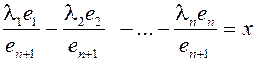Date: 2015-09-03; view: 873; Нарушение авторских прав