Диагонализация матрицы линейного оператора

Диагонализация матриц линейных операторов – это процесс перехода к новому базису, в котором матрица данного оператора имеет диагональный вид.

Теорема: Для того чтобы матрица линейного оператора имела диагональный вид в некотором базисе, необходимо и достаточно, чтобы этот базис состоял из векторов данного оператора..(Утв1 Утв.2).

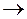Если матр. диагон., то базис состоит из собственных векторов

Д-во: Пусть матрица 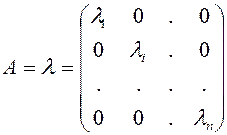, 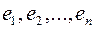- соотв. базис.

Покажем, что векторы 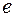являются собственными .

если базис состоит из собственных векторов…

Пусть базисный вектор 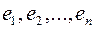является собственным вектором, отвечающий собственным значениям матрицы . По определению матрицы линейного оператора столбцы – это образы базисных векторов при соответствующих отношениях.

Таким образом 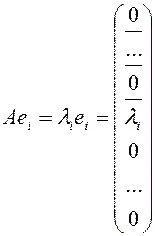. Диагональный вид матрицы линейного оператора (в базисе есть собственный вектор) называемый каноническим.

Есть 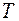- матрица перехода к базису, состоящему из собственных векторов, то матрицы, соответствующая диагональному виду, .

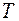состоит из собственных векторов данного оператора, записывается по столбцам. Базис из соотв. вект. сущ. у самосопряженного оператора, который имеет симметричную матрицу 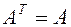. В этом случае существует ортонормированный базис, состоящий из собственных векторов; переход к такому базису - это переход от ортонормированного базиса к ортонормированному .

Date: 2015-09-03; view: 6281; Нарушение авторских прав