Определение подпространства линейного векторного пространства, критерий подпространства. Примеры подпространства

Определение линейного векторного пространства и следсвия из аксиом.

Множество V, в котором определены операции сложения(внутренняя операция) его элементов и умножения (внешняя операция) элементов множества на произвольные числа из R и эти операции удовлетворяют указанным выше аксиомам, называются вещественным линейным или векторным пространством.

Аксиомы:

1. x+y = y+x

2.

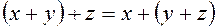
3. в множестве V существует элемент (который будем называть нулевым и обозначать О), такой, что x+О = x

4. Для каждого элемента 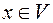существует элемент(который будем называть противоположным элементу x и обозначать –x), такой, что .

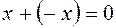5. Для любого 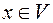1x = x.

6.

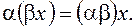
7.

8. .

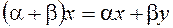Определение подпространства линейного векторного пространства, критерий подпространства. Примеры подпространства.

Множество 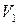элементов линейного пространства называется подпространством пространства, если выполняются следующие условия:

1. В множестве 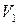операции сложения элементов и умножения элемента на число определяются так же, как в множестве V.

2. если x, 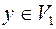,то ;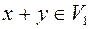

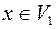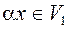3. если , то , где 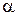- вещественное число, когда V- вещественное пространство, и комплексное, когдаV- комплексное.

Теорема: Пусть 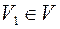, где V- линейное пространство, 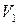является подпространством, тогда и только тогда, когда выполняются следующие условия:

1. (т.е. операция сложения должна быть замкнута на )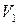

2. 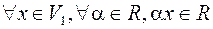(т.е. операция умножения на число замкнута на )

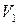Доказательство: Все аксиомы, кроме 3., 4., выполняются очевидным образом, поскольку они верны не только для множества 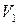, но и для всего множества 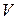, содержащее .

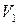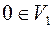
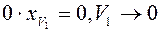
Date: 2015-09-03; view: 1057; Нарушение авторских прав