Обратный оператор. Его существование и линейность. Матрица обратного оператора

Пусть 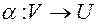. Будем считать, что 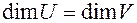(размерность). - невырожденный оператор, т.е. .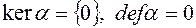

Невырожденный оператор имеет невырожденную матрицу, т.е., если А – матрица этого оператора, то матрица невырожденная .

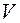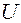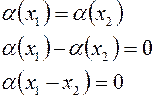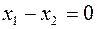Отметим, что осуществляет взаимно однозначное отображение между векторами пространства и . Это значит, что разные векторы имеют различные образы. Действительно, предположим что . Т.к. - невырожденная, то , т.е. 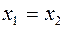. Учитывая, что 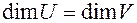, образ - это все пространство . Тогда для каждого , существует единственный верный элемент такой, что можно определенно отображать 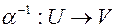. 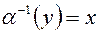, где .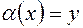

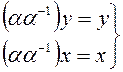- свойства обратного отображения.

Можно показать, что отображение является линейным.

.

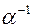- обратный оператор к оператору . Если А – матрица оператора , то 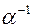имеет матрицу . .

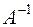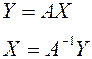19. Сопряженные операторы. Теорема о существовании, единственности и линейности (б/д). Свойства сопряженного оператора и его матрица. Самосопряженные операторы.

Пусть 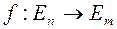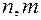- размерность. Определитель 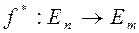называется сопряженным к оператору 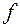, если 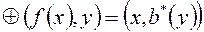, если для .

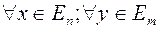Теорема: Сопряженный оператор для всякого оператора 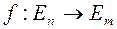существует единственный и линейный.

Свойства:

.

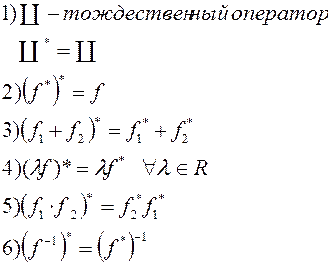Матрица сопряженного оператора. Пусть 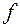имеет матрицу А; 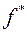имеет матрицу 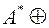в матричном виде: , 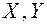- столбцы координат. .

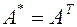(из свойств скалярного произведения).

Таким образом, матрица сопряженного оператора равна трансформированной матрице исходного оператора.

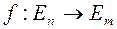называется самосопряженной, если . Матрица у такого оператора симметрична.

21. Ортогональные операторы. Теорема о критериях ортогонального оператора (б/д). Свойства ортогонального оператора и его матрица.

Пусть 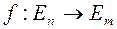. Оператор 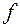называется ортогональным, если скалярное произведение .

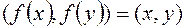Следующие утверждения равносильны:

1) 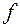- ортогональный оператор;

2) 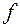переводит ортонормированный базис в ортонормированный (образы базисных элементов снова образовывают ортонормированный базис).

3) (Сопряженный оператор совпадает с обр. оператором).

Свойства:

1) Тождественный оператор ортогонален;

2) Произведение ортогональных операторов является ортогональным

3) Обратный оператор к ортогональному также является ортогональным.

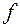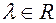4) Пусть - ортогон., - ортогональн., где это равносильно тому что

Теорема. Для того чтобы оператор 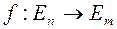был ортогональным, необходимо и достаточно, чтобы его матрица в ортонормированном базисе была ортогональна.

Матрица ортогонального вектора. Для ортогонального оператора 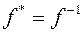(по определению). Если А – матрица 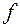, то 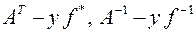. Для матриц (у ортогонального оператора обратной матрицей явл. Трансформированная матрица): .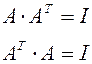

Свойство матрицы :

Произведение всякого столбца этой матрицы на себя равно 1, а произведение всякого столбца на другой столбец равно 0. Такие матрицы называются ортогональными. Столбцы ортогональной матрицы могут служить базисом соответствующего Евклидова пространства.

Date: 2015-09-03; view: 2504; Нарушение авторских прав