Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Уравнение Бернулли
|
|
Еще одной разновидностью уравнения энергии является обобщенное уравнение Бернулли для газа [5]. От уравнений (2.4) или (2.5) оно отличается тем, что все входящие в него слагаемые имеют механическое происхождение. Это уравнение можно получить следующим путем. Воспользуемся тем же самым приемом, с помощью которого выше было получено дифференциальное уравнение энергии (2.6) и представим уравнение (2.3) в дифференциальном виде:
CvdT + d(p/ρ) + d(w2/2) - dQе + dL = 0. (2.7)
Количество тепла Q, воспринимаемое газом, и количество тепла Qе, подводимое к нему извне, в общем случае не одинаковы: существует еще тепло тренияQ r, которое выделяется вследствие трения газа о стенки, внутреннего трения (возникающего между слоями, движущимися с разными скоростями), образования вихрей и т.п. Это тепло также воспринимается газом. Поэтому
Q = Qе + Qr = Qе + Lr. (2.8)
Тогда
dQе = dQ – dLr, (2.9)
где Lr — работа трения (в системе единиц СИ Qr=Lr).
Количество тепла, воспринимаемое газом, можно определить с помощью уравнения первого закона термодинамики
dQ = CvdT + pdv. (2.10)
Подставив это выражение в формулу (2.9), получим
CvdT = dQe + dLr -pdv. (2.11)
Кроме того,
d(p/ρ)=d(pv)=pdv+vdp/. (2.12)
После подстановки формул (2.11) и (2.12) в уравнение энергии (2.7) и замены удельного объема через плотность v=1/ρ получаем уравнение Бернулли для газа в дифференциальной форме
dp/ρ+d(w2/2)+dL+dLr=0. (2.13)
При решении конкретных задач уравнение Бернулли интегрируют в пределах от начального сечения расчетного участка до конечного
12∫(dp/ρ)+(w22- w12)/2 + L+ Lr=0. (2.14)
Если в процессе решения нужно получить параметры потока в каком-нибудь промежуточном сечении расчетного участка, то при интегрировании это сечение принимается за конечное. При решении можно брать неопределенный интеграл. Константа интегрирования определяется тогда из граничных условий, в качестве которых обычно берут условия на входе в расчетный участок.
Для того чтобы вычислить ∫(dp/ρ), надо знать зависимость между р и ρ, т.е. иметь уравнение термодинамического процесса, при котором происходит течение газа, например уравнение политропы p/ρn=const. Если известен термодинамический процесс, то известен и показатель политропы. При политропном процессе интегрирование дает
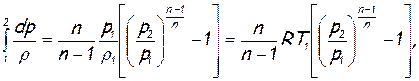(2.15)
при изотермном процессе (n=1)
12∫(dp/ρ)=(p1/ρ1)ℓn(p2/p1)=RT1ℓn(p2/p1). (2.16)
Сопоставляя между собой уравнение энергии и уравнение Бернулли, например (2.4) и (2.14), можно заметить, что первое учитывает внешнее тепло, но не содержит работы трения в явном виде, тогда как второе не содержит в явном виде внешнего тепла, но учитывает работу трения. Поэтому создается впечатление, что эти уравнения не учитывают всех особенностей течения. В действительности это не так. Хотя работа трения и не входит явно в уравнение энергии, но ее влияние сказывается, прежде всего, на температуре Т2.
Что касается уравнения Бернулли, то в нем внешнее тепло учитывается при вычислении ∫(dp/ρ), а именно, от количества подведенного тепла зависит величина показателя политропы n.
& [1] с.24…34. [3] с.31…36. [4] с.39..42. [5] с.412…415.
& [6] с.130…133. [7] с.47…48. [8] с.93…94.
Рассмотрим уравнения энергии для частных случаев течения газа.
Date: 2015-09-03; view: 848; Нарушение авторских прав