
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Уравнение сохранения энергии для стационарного поточного процесса
|
|
Большое значение в газовой динамике имеет закон сохранения энергии. Он, как известно, констатирует тот факт, что
энергия не возникает и не исчезает, а только превращается
из одного вида в другой.
Следовательно, составив баланс энергии для какого-нибудь количества газа, например, для единицы массы, можно найти соотношение между различными составляющими энергии. Такая математическая запись энергетического баланса и представляет собой уравнение энергии.
Составление баланса энергии рассмотрим на примере газотурбинной установки, схема которой изображена на рисунке 6. Баланс энергии можно составить и для любой другой схемы течения. Пример с газотурбинной установкой взят потому, что в нем присутствуют все составляющие энергетического баланса, рассматриваемые в большинстве подобных газодинамических задач. Кроме того, это типичный пример так называемого поточного процесса. Конечно же реальный процесс течения газа в газотурбинной установке не является стационарным в полном смысле этого понятия, но при известной степени идеализации в контексте решаемой задачи он вполне может рассматриваться как «квазистационарный».
Через входное сечение 1 воздух из атмосферы поступает в компрессор, где сжимается и подается в камеру сгорания. Туда же, в камеру сгорания, поступает жидкое топливо, которое, смешавшись с воздухом, сгорает, выделяя большое количество тепла. Таким образом, в турбину из камеры сгорания поступают образовавшиеся там продукты сгорания с высокой температурой и высоким давлением. В турбине они расширяются, производя работу — вращая ротор. Часть работы турбины при помощи вала передается на вращение компрессора, другая часть отдается потребителю. Отработанные газы покидают турбину, выходя через сечение 2.

Параметры воздуха на входе в газотурбинную установку - T1, p1, ρ1,,w1;
на входе - Т2, p2, ρ2, w2.
Энергия поступающего воздуха, отнесенная к единице массы, обозначена Е1 , энергия выходящего газа — Е2.
Подведенное тепло обозначено Qе. Индекс «е» означает, что тепло подводилось извне (externus – лат. внешний, посторонний).
Здесь нет никакого противоречия: несмотря на то, что сгорание происходило внутри камеры и тепло, подогревающее газ, выделялось именно там, энергия эта была внесена снаружи в скрытом виде, вместе с топливом. Следовательно, поскольку не ставится задача изучения физико-химических процессов горения, а рассматриваются только явления газодинамического характера, то можно считать, что тепло в количестве Qе было внесено в камеру сгорания снаружи.
Работа на валу установки, отданная потребителю, обозначена L. Она также отнесена к единице массы проходящего через установку воздуха.
На рисунке 7 изображена упрощенная схема течения. На расчетном участке между сечениями 1 и 2, так же как и в предыдущем случае, подводится тепло и отводится механическая работа. Следовательно, для упрощенной схемы баланс энергии будет таким же, как и для газотурбинной установки, но пользоваться этой схемой проще и удобнее.
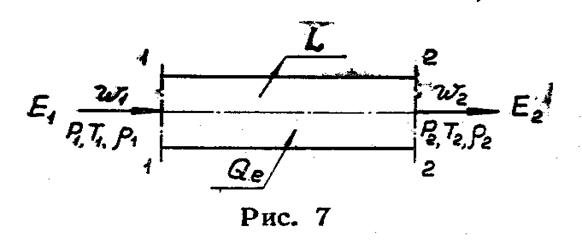
Баланс энергии для рассматриваемой схемы течения можно записать следующим уравнением:
Е1 - Е2 + Qе - L = 0. (2.1)
Далее необходимо расшифровать, что подразумевается под полным запасом энергии единицы массы газа Е. При этом нужно иметь в виду, что в «полный запас энергии» нет надобности включать все ее составляющие (например, химическую, электрическую, внутриядерную); вполне достаточно принимать в расчет только те ее виды, которые могут превращаться один в другой в пределах изучаемых газодинамических задач. Тогда можно записать, что
E= u + p/ρ + w2/2 + gz, (2.2)
где u – внутренняя энергия единицы массы газа;
p/ρ – потенциальная энергия давления единицы массы газа;
w2/2 – кинетическая энергия единицы массы газа;
gz– потенциальная энергия положения (уровня) единицы массы газа;
z – геометрическая высота;
g – ускорение силы тяжести.
Все указанные величины измеряются в единицах работы на единицу массы, а именно в дж/кг или, что то же самое, в м2/сек2 (в системе СИ).
Подставив в уравнение (2.1) значения Е1 и Е2, выраженные с помощью уравнения (2.2), и учитывая, что разность внутренних энергий u1 – u2 = Cv(T1-Т2), получим
Cv(T1-Т2) +p1/ρ1-p2/ρ2 +(w12- w22)/2+g(z1-z2) +Qе-L= 0. (2.3)
Это и есть уравнение энергии для одномерного потока или для элементарной струйки. Оно показывает, как происходит изменение внутренней энергии Cv(T1-Т2), потенциальной энергии давления p1/ρ1-p2/ρ2 , кинетической энергии (w12- w22)/2, потенциальной энергии положения g(z1-z2) в результате действия подведенного извне тепла Qе и работы L, отданной газом внешнему потребителю. Изменение внутренней энергии связано с изменением температуры газа, кинетической энергии — с изменением скорости потока, потенциальной энергии уровня — с изменением высоты положения рассматриваемой массы газа над плоскостью, принятой за начало отсчета. Что касается изменения потенциальной энергии давления, то оно требует специальных разъяснений.
На рисунке 8 изображен расчетный участок потока, ограниченный на входе сечением 1 и на выходе — сечением 2.
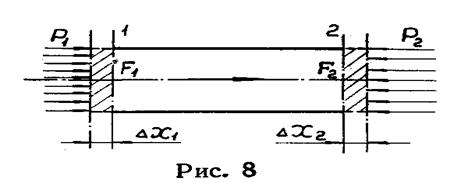
При входе газа через сечение 1 силы внешнего давления р1F1, вталкивая в расчетный, участок объем газа F1Δx1, совершают работу p1F1Δx1.
При выходе из расчетного участка, через сечение 2 объем газа F2Δx2 совершает работу против сил внешнего давления p2F2Δх2. Поделив эти работы на массу газа в соответствующих объемах, получим
Lвт= p1F1Δx1/ ρ1F1Δx1= p1/ρ1 ,
Lвыт= p2F2Δx2/ ρ2F2Δx2= p2/ρ2.
Следовательно, p1/ρ1-p2/ρ2=Lвт-Lвыт представляет собой разницу работ вталкивания и выталкивания единицы массы газа. Эта величина характеризует накопление (если p1/ρ1>p2/ρ2) потенциальной энергии давления или расходование ее (если p1/ρ1<p2/ρ2 ) потоком газа, находящимся внутри расчетного участка.
Изменение потенциальной энергии уровня g(z1-z2) в задачах, связанных с расчетом теплоэнергетических машин или установок, как правило, составляет пренебрежимо малую величину по сравнению с другими членами уравнения энергии. Оно обычно не превышает 50…100 м2/сек2, тогда как другие члены имеют порядок 10 000…100 000 м2/сек2. Поэтому во всех дальнейших рассуждениях и расчетах величина g(z1-z2) будет отброшена. Однако, нужно обратить внимание на задачи такого рода, как расчет вентиляционных систем шахт, в которых изменение потенциальной энергии уровня весьма велико и может превышать значения других членов уравнения энергии. В этих случаях величина g(z1-z2) должна учитываться обязательно.
Уравнению энергии можно придать другую, во многих случаях более удобную для расчетов форму. Преобразуем сумму членов
Cv(T1-Т2) +p1/ρ1-p2/ρ2 = (CvT1+p1/ρ1) -(CvT2+p2/ρ2)=
=(CvT1+RT1) -(CvT2+ RT2)= (Cv +R)(T1-Т2) = Cp(T1-Т2),
используя известное из термодинамики соотношение Cp–Cv=R, и подставим полученное выражение в уравнение (2.3). Тогда уравнение энергии можно записать более компактно
Cp(T1-Т2) + (w12- w22)/2 + Qе - L = 0, (2.4)
а главное, три термодинамических параметра p, ρ и T теперь можно заменить всего лишь одним – энтальпией h=CрТ. («Три в одном»!)
h1-h2 + (w12- w22)/2 + Qе - L = 0. (2.5)
Этот вид уравнения энергии называют еще уравнением энтальпии или теплосодержания, так как в него входит энтальпия h.
В уравнении энергии принято следующее правило знаков. Подведенное внешнее тепло считается положительным, а отведенное — отрицательным; работа, совершенная газом и отведенная к внешнему потребителю, — положительной, а подведенная к газу извне и затраченная на его сжатие — отрицательной. Таким образом, в нагревателе газа (камере сгорания) тепло считается положительным, в охладителе — отрицательным; работа, получаемая в турбине, — положительной, а затрачиваемая на вращение компрессора — отрицательной. Это правило знаков согласуется с уравнением первого закона термодинамики.
Уравнение энергии часто применяется в дифференциальной форме. Чтобы получить его в этой форме, воспользуемся таким приемом. Будем мысленно приближать второе сечение к первому, уменьшая длину расчетного участка до бесконечно малой величины. Тогда в пределе получим вместо Qе и L соответственно dQе и dL, авместо конечных разностей Т1–Т2 и (w12- w22)/2 получим соответствующие дифференциалы – dТ и – d(w2/2).
В последних двух выражениях знак минус появился потому, что берутся бесконечно малые разности T1—Т2 и (w12- w22)/2, а не T2—Т1 и (w22- w12)/2.
Подставив это в уравнение энергии (2.4) и поменяв знаки на обратные, получим уравнение энергии в дифференциальной форме или дифференциальное уравнение энергии
CpdT + d(w2/2) - dQе + dL = 0. (2.6)
***
Если сопоставить выражение для полного запаса энергии (2.2)
E= u + p/ρ + w2/2 + gz,
с левой частью уравнения Бернулли, которая также представляет величину полного запаса энергии единицы массы несжимаемой жидкости
p/ρ + w2/2 + gz = const,
то можно заметить, что в случае газа дополнительно введена величина внутренней энергии u. Это объясняется тем, что при ρ≠соnst тепловые процессы оказывают влияние на плотность газа, и так как его расширение или сжатие связано с работой, то в конечном итоге это влияние распространяется на механические составляющие энергии. Таким образом, в уравнениях энергии (2.4) и (2.5) присутствуют величины, имеющие как механическое, так и тепловое (калорическое) происхождение.
& [1] с.11…19. [3] с.31…36. [4] с.53..54.
Date: 2015-09-03; view: 1901; Нарушение авторских прав