Математическое моделирование процесса движения

Зададимся для системы с 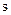степенями свободы минимально необходимым числом обобщенных координат 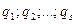. Нужные для кинематического анализа координаты отдельных точек 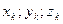(избыточные координаты) определяются из уравнений кинематических связей:

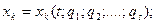
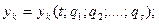
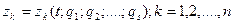(9.1)

Или в векторной форме

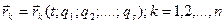(9.2)

Движение системы приводит к изменению обобщенных координат 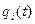и к появлению обобщенных скоростей 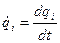и обобщенных ускорений 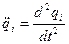. Размерности этих величин могут отличаться от размерностей скоростей 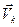и ускорений точек 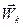, так как в число обобщенных координат могут входить углы поворотов.

Необходимые для кинематического анализа скорости и ускорения характерных точек получают путем дифференцирования по времени выражения (9.2):

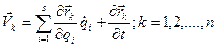; (9.3)

.

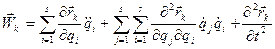Особенность рассмотренного в (9.1) – (9.3) случая заключается в том, что уравнения связей (9.1) позволяют найти аналитические выражения избыточных координат 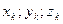через обобщенные .

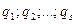Чаще всего сделать это не удается и возникает система трансцендентных уравнений относительно избыточных координат вида

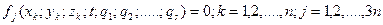
(9.4)

Дифференцируя (9.4) по времени, получают линейную относительно избыточных скоростей систему алгебраических уравнений:

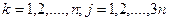(9.5)

Из (9.5) получают тем же приемом дифференцирования линейную систему алгебраических уравнений относительно избыточных ускорений :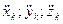

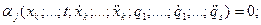
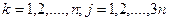(9.6)

Основные трудности кинематических исследований, опирающихся на выражения (9.4) – (9.6), заключаются в многократном решении системы трансцендентных уравнений (9.4).

В известной мере эти трудности можно обойти, если применить к решению трансцендентных уравнений (9.4) метод продолжения по параметру. В этом методе считается известным одно из решений 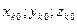системы уравнений (9.4), соответствующее известному состоянию (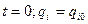). Как правило, это решение удается получить в особых положениях точек механической системы, когда ее конфигурация поддается простому геометрическому анализу. В крайнем случае, один раз придется решить систему (9.4) любым другим численным методом либо графически. Зная решение 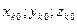, находят значения скоростей и ускорений .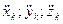

Значения избыточных координат 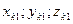через малый промежуток времени 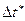находят интегрированием по методу Эйлера:

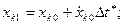
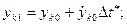(9.7)

.

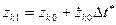Критерием правильности выбора шага 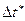является точность 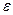выполнения исходных трансцендентных уравнений

.

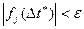Так, на каждом шаге решение трудоемкой задачи определения корней трансцендентных уравнений (9.4) заменяется более простой задачей численного интегрирования во времени (9.7). При этом, правда, на каждом шаге необходимо решать систему линейных относительно алгебраических уравнений (9.5). Но эта задача решается достаточно эффективно даже при сотнях искомых неизвестных.

ПРИМЕР 9.1. Плоский механизм (рис.9.6) с одной степенью свободы составлен из звеньев 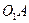и 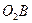, соединенных ползуном, и звена 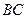, присоединенного шарнирно. Ведущее звено 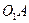движется по заданному закону 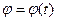(рад.), где 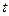-время в секундах. Заданы размеры всех звеньев. Написать алгоритм расчета глобальных кинематических характеристик всех звеньев механизма и локальных кинематических характеристик всех обозначенных точек при возрастании времени от нуля до значения T с шагом .

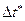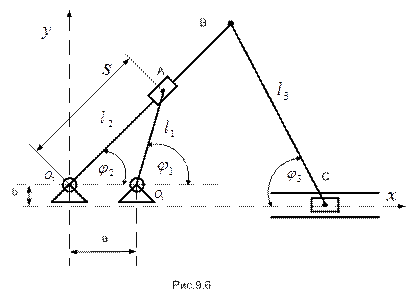
РЕШЕНИЕ. Уравнения кинематических связей рассматриваемого механизма в векторной форме имеют вид

;

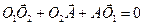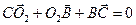. (9.8)

За избыточные обобщенные координаты выберем параметры 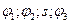. Тогда уравнения (9.8) в проекциях на оси координат 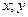примут вид

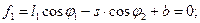
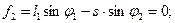(9.9)

.

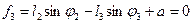Все связи стационарны.

В том случае, когда система (9.9) допускает получение дважды дифференцируемых по времени аналитических зависимостей вида

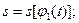
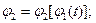
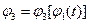, расчет глобальных кинематических характеристик звеньев и локальных кинематических характеристик их точек может быть выполнен для интересующих нас моментов времени ( где 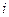=1,2,… - целые числа) по формулам глав 3 и 4. Для последующего анализа результаты расчетов сводят в таблицу либо используют для построения графиков.

В том случае, когда система (9.9) не допускает получения необходимых аналитических зависимостей, ее следует, как предлагалось выше, продифференцировать по времени и представить в виде системы линейных дифференциальных уравнений относительно неизвестных производных (с переменными в процессе движения коэффициентами):

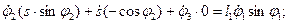
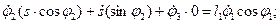(9.10)

.

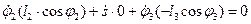Любым из известных способов (например, методом Крамера) можно получить выражения для обобщенных скоростей как решение (9.10):

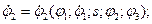
(9.11)

.

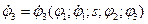Выражения для обобщенных ускорений можно получить, например, продифференцировав (9.11) по времени:

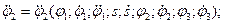
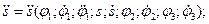(9.12)

.

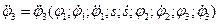Начальные значения избыточных обобщенных координат находят как решение (9.9) каким-либо методом (например, достаточно аккуратно выполнив чертеж механизма при 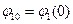и замерив на нем величины 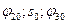). Подставив вычисленные 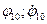и замеренные величины 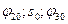в (9.11), найдем для начального момента времени избыточные обобщенные скорости 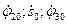. Подставив вычисленные и найденные избыточные обобщенные координаты и скорости в (9.12), получим для начального момента времени избыточные обобщенные ускорения.

Для решения возникшей задачи Коши воспользуемся методом численного интегрирования Эйлера:

где - решение уравнения вида 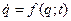, удовлетворяющее начальному условию 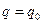при

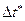- шаг интегрирования.

Оценка погрешности на каждом шаге интегрирования выполняется по значению невязки 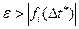, т.е.проверкой точности выполнения уравнений связей (9.9). При неудовлетворительной точности значение шага интегрирования уменьшают вдвое и т.д.

Для последующего анализа результаты расчета сводят в таблицу либо используют для построения графиков.

Список литературы

1. Тарг С.М.Краткий курс теоретической механики. Высшая школа, Москва, 1986 г.

2. Мещерский И.В. Задачи по теоретической механике. Лань, Москва, 2002 г.

3. Мелконян А.Л., Митрофанов В.П., Пановко Я.Г., Рощанский В.И., Черныш А.А. Теоретическая механика. Часть 1. Кинематика. Учебное пособие, Издательство ЛКИ, Ленинград, 1989 г.

Учебное пособие

МЕЛКОНЯН Армен Левонович, Черныш Александр Алексеевич

ТЕОРЕТИЧЕСКАЯ МЕХАНИКА. КИНЕМАТИКА

Редактор

Корректор

Верстка

Date: 2015-09-03; view: 426; Нарушение авторских прав