Ускорение точки при сложном движении

Для того, чтобы получить соотношение, связывающее ускорения точки в различных системах отсчета, продифференцируем выражение (7.9) по времени:

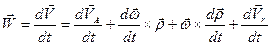. (7.11)

Абсолютные производные радиуса-вектора 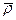и вектора относительной скорости с учетом формул (7.11) запишем в виде

;

.

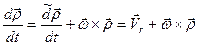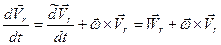Подставив полученные выражения в (7.11) и сгруппировав их, получим

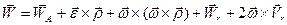. (7.12)

Сумма первых трех слагаемых в (7.12) есть ускорение той точки подвижной координатной системы, которая в данный момент времени совпадает с точкой М, т.е. переносное ускорение .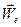

Пятое слагаемое носит название поворотного ускорения или ускорения Кориолиса; ниже оно обозначается 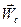. После соответствующих преобразований уравнение (8.12) примет вид

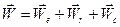. (7.13)

Формула (7.13) выражает теорему Кориолиса: абсолютное ускорение точки равно сумме переносного, относительного ускорений и кориолисова, равного

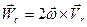. (7.14)

Модуль ускорения Кориолиса 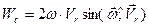, а направление определяется по правилу векторного произведения.

Ускорение Кориолиса равно нулю, если:

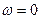- (переносное движение поступательное либо равенство справедливо в некоторые моменты времени),

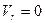- (равенство справедливо в некоторые моменты времени),

- (векторы, входящие в (7.14) параллельны).

Заметим, что в формулах (5.10) для вычисления ускорения точки при плоскопараллельном движении тела имеет место первый из оговоренных случаев.

После формулы (7.10) наличие последнего слагаемого в формуле (7.13) может вызвать недоумение. Ниже на простом примере показано, что в общем случае .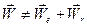

Рассмотрим круглую платформу радиуса R, вращающуюся вокруг своего центра О с постоянной угловой скоростью 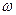(рис.7.2). По краю платформы пустим точку М так, чтобы она все время находилась напротив маяка А, установленного на неподвижном основании. Очевидно, что в неподвижной системе отсчета точка М покоится, т.е. ее абсолютные скорость и ускорение равны нулю.

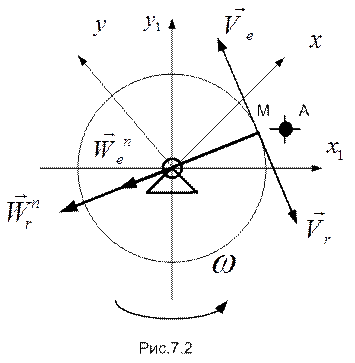
Принимая движение точки М по платформе за относительное, а движение совпадающей с ней точки – за переносное, имеем

; ; .

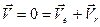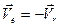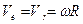Ускорения точки М в указанных движениях будут равны своим нормальным составляющим. Последние направлены от точки М к центру платформы и равны 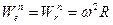. Их сумма не равна нулю, что противоречит здравому смыслу (неподвижность точки М).

Появление ускорения Кориолиса объясняется взаимовлиянием переносного и относительного движений, которое отсутствует при независимом рассмотрении картин составляющих движений.

Задачи на сложное движение точки подразделяются на два типа: в первом по известным переносному и относительному движениям определяют абсолютное, во втором известное абсолютное движение раскладывают на интересующие составляющие.

ПРИМЕР 7.1 (задача 23.31 из [2]). Шайба М движется по горизонтальному стержню ОА так, что 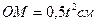. В то же время стержень вращается вокруг вертикальной оси, проходящей через точку О, по закону 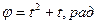. Определить радиальную и трансверсальную составляющие абсолютной скорости и ускорения шайбы в момент времени .

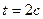РЕШЕНИЕ. Примем за относительное движение шайбы ее движение вдоль стержня ОА по закону 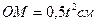; картина этого движения (КОД) и его кинематические характеристики, вычисленные для момента времени 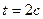, изображены на рис.7.3.

; ; ;

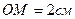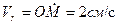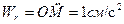Переносным движением шайбы М будет движение точки стержня, находящейся в рассматриваемый момент времени под шайбой. Для расчета ее скорости и ускорения сначала необходимо рассчитать угловую скорость и угловое ускорение стержня ОА:

; ;

; ; .

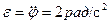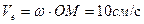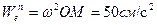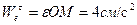Картина переносного движения (КПД) и вычисленные для него кинематические характеристики изображены на рис.7.4.

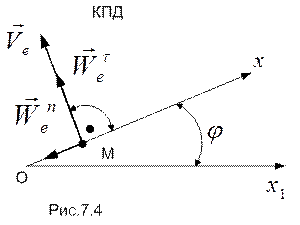
Ускорение Кориолиса равно 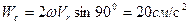, его направление см. на рис.7.3.

Теперь вычислим радиальные (проекции на ось Оx подвижной координатной системы) составляющие абсолютной скорости и абсолютного ускорения:

; .

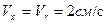Трансверсальные (проекции на ось Oy подвижной координатной системы) составляющие абсолютной скорости и абсолютного ускорения будут

; .

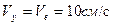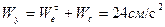Рассмотренная задача позволяет лучше понять формулы для расчета проекций скорости и ускорения точки на оси полярной координатной системы, полученные в параграфе 1.2.б формальным дифференцированием.

ПРИМЕР 7.2 (задача 22.3 из [2]). Корабль, проходящий точку А, движется с постоянной по модулю и направлению скоростью 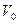. Под каким углом 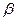к прямой АВ надо начать двигаться катеру из точки В, чтобы встретиться с кораблем, если скорость катера постоянна по модулю и направлению и равна 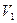? Линия АВ составляет угол 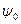с перпендикуляром к курсу корабля.

РЕШЕНИЕ. На рис.7.5 схематично изображена акватория, где движутся точки А (корабль) и В (катер). Точкой С обозначено место их предполагаемой встречи.

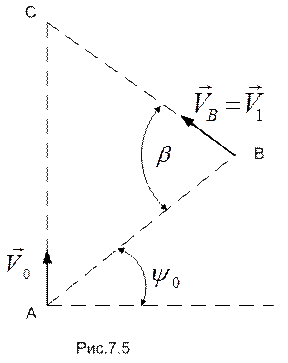
Представим прямолинейное движение катера (по прямой АС) как сложное, состоящее из переносного движения вместе с кораблем (поступательное движение по прямой АС) и относительного – по отношению к кораблю (в момент старта катера - движение по прямой АВ). Тогда

.

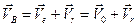В этом треугольнике известны модули скоростей корабля 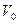и катера 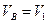, а так же угол 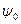между скоростью корабля и линией АВ. Теорема синусов позволяет записать соотношение

.

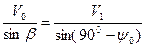Тогда .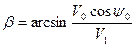

Date: 2015-09-03; view: 1027; Нарушение авторских прав