Сложение поступательных движений

Зададим 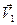- скорость поступательного движения тела относительно подвижной системы отсчета и 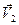- скорость поступательного движения подвижной системы отсчета относительно неподвижной. Для скорости произвольной точки М тела применим формулу (7.10):

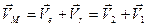. (8.1)

Равенство (8.1) справедливо для всех точек тела, таким образом, при сложении поступательных движений твердого тела результирующее движение будет так же поступательным; скорость результирующего движения равна сумме скоростей составляющих движений. То же самое справедливо и для его ускорения.

При необходимости найти результат сложения нескольких поступательных движений надо выполнить их последовательное сложение.

8.2. Сложение вращений вокруг пересекающихся осей *

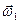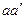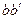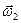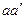Рассмотрим тело Р, вращающееся с угловой скоростью вокруг оси , которая, в свою очередь, вращается вокруг неподвижной оси с угловой скоростью ; оси и 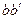пересекаются в точке О

(рис.8.1). Очевидно, что в таком случае точка О является неподвижной точкой, а тело Р совершает сферическое движение. Покажем, что сумма

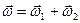(8.2)

является вектором мгновенной угловой скорости сферического движения.

Для этого выберем произвольную точку М, принадлежащую телу Р, и определим ее скорость как результат сложения скоростей в переносном и относительном движениях. При этом движение точки М вместе с телом Р вокруг оси 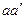примем за относительное движение (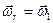), а вращение вместе с осью 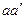вокруг оси 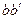- за переносное (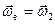). Тогда

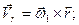
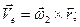
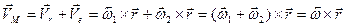. (8.3)

Формула (8.3) совпадает с формулой (4.5), т.е. 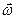представляет собой вектор угловой скорости сферического движения. Определение глобальных и локальных кинематических характеристик сферического движения подробно рассмотрено в главе 4. Однако в ряде ситуаций, когда положение осей относительного и переносного вращений достаточно очевидно (см. рис.4.7 и 4.8), расчет кинематических характеристик приемами, полученными в главах 7 и 8, оказывается более простым.

ПРИМЕР 8.1. Определить кинематические характеристики точки А гироскопа - успокоителя качки (см. главу 4 и рис.4.5), рассматривая движение диска как сложное.

РЕШЕНИЕ. Движение диска вокруг собственной оси z с угловой скоростью 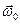примем за относительное (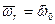), а вращение вокруг неподвижной горизонтальной оси – за переносное (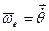). Оба вращения можно заменить одним вращением вокруг мгновенной оси с угловой скоростью .

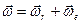Абсолютная скорость точки А диска, совершающего сложное движение, будет

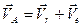, где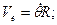

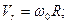
откуда .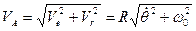

Абсолютное ускорение точки А диска

,

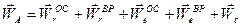где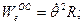

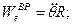
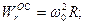
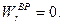
Ускорение Кориолиса равно нулю, так как векторы и параллельны.

Как следует из рис.8.2, модуль ускорения точки А будет

.

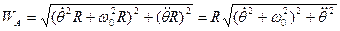Полученные результаты совпадают с результатами, полученными в параграфе 4.3.

8.3. Сложение вращений вокруг параллельных осей *

Покажем, что формула (8.2) пригодна для случая, когда составляющие движения представляют собой вращения вокруг параллельных осей.

Рассмотрим платформу Р, вращающуюся с угловой скоростью 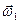вокруг оси 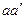, которая, в свою очередь, вращается вокруг параллельной ей оси 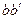с угловой скоростью 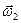. На рис.8.3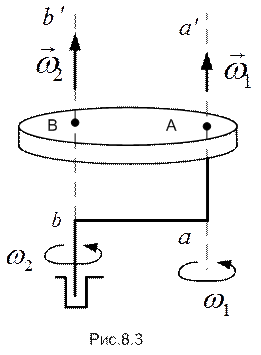

изображен случай, когда направления векторов угловых скоростей совпадают. Точки пересечения осе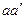й и 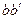с платформой обозначены А и В.

Определим скорости этих точек, воспользовавшись формулой (7.10). Для этого представим абсолютное движение платформы как сумму относительного (вращение с угловой скоростью 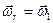вокруг оси 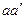) и переносного (вращение с угловой

скоростью 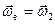вместе с осью 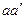вокруг оси 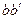). Точка А

участвует только в переносном движении, поэтому

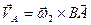. (8.4.a)

Точка В участвует только в относительном движении, следовательно:

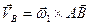. (8.4.б)

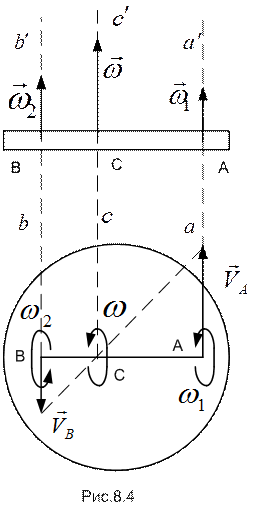
Векторы 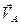и 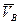параллельны и направлены в противоположные стороны (рис.8.4).

В таком случае на отрезке АВ существует точка С (м.ц.с.), скорость в которой равна нулю. Ось, проходящая через м.ц.с. и параллельная осям 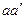и 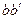- мгновенная ось вращения.

Составим пропорцию:

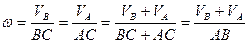(8.5)

и согласно формулам (8.4)

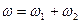, (8.6)

Т.е. в рассмотренном случае результирующее движение является вращением вокруг мгновенной оси с угловой скоростью, равной сумме угловых скоростей составляющих движений.

Если составляющие вращения платформы противоположны по направлению, то построение будет соответствовать рис.8.5.

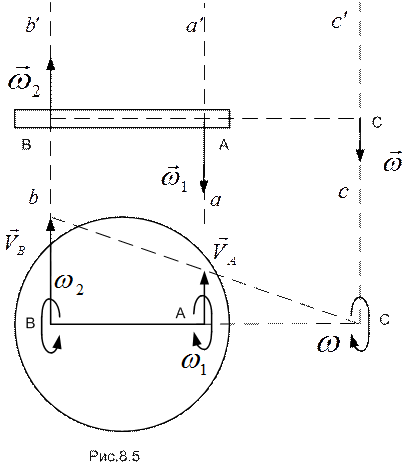
Точка С (м.ц.с.) расположена вне отрезка АВ; угловая скорость результирующего вращения равна

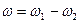, (8.7)

а его направление совпадает с направлением той составляющей, модуль угловой скорости которой наибольший.

Векторные записи формул (8.6) и (8.7) одинаковы и эквивалентны формуле (8.2).

В частном случае, когда угловые скорости составляющих движений равны и противоположно направлены, по формуле (8.7) 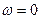. Это свидетельствует о том, что результирующее движение тела мгновенно-поступательное (если угловые скорости постоянны по модулю, то движение тела поступательное). Такая совокупность вращений называется парой вращений, а векторы образуют пару угловых скоростей. При этом скорость любой точки тела равна

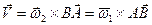, (8.8)

где АВ – плечо пары угловых скоростей.

Если модули угловых скоростей составляющих вращений переменны во времени, оказывается переменным, в общем случае, и модуль угловой скорости результирующего вращения 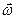. Возникающий при этом вектор углового ускорения 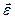имеет с вектором 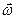общую линию действия, а его модуль равен 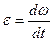. Нетрудно заметить, что результирующее движение тела будет плоскопараллельным (см. главу 5), а векторы 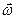и 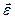входят в состав его глобальных кинематических характеристик. Однако в ряде ситуаций использование такого подхода оказывается более удобным и менее трудоемким (например, в кинематических расчетах планетарных и дифференциальных передач).

8.5. Кинематика планетарных и дифференциальных передач*

Планетарной называется передача (рис.8.6), в которой зубчатое

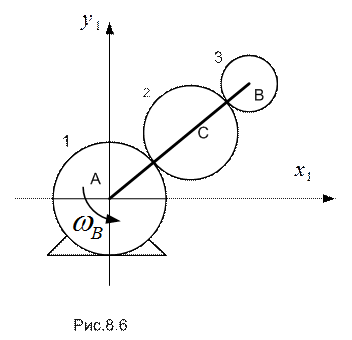
колесо 1 неподвижно, а оси остальных колес, находящихся в последовательном зацеплении, укреплены на кривошипе АВ, вращающемся вокруг неподвижного центра (движения колес напоминают движение планет: - вращение вокруг собственной оси и движение оси по окружности вокруг Солнца). В литературе по механике для кривошипа АВ иногда используют термин водило.

Дифференциальной называется передача, изображенная на рис.8.8.а, если в ней зубчатое колесо 1 вращается независимо от вращения кривошипа АВ.

Расчет планетарной передачи заключается в нахождении соотношений между угловой скоростью водила и угловыми скоростями колес; для дифференциальной – между угловыми скоростями водила и колеса 1 и угловыми скоростями колес. Очевидно, что радиусы колес должны быть известны. Если в получаемых соотношениях фигурируют отношения радиусов, их можно заменить отношениями чисел зубьев соответствующих колес (в силу пропорциональности числа зубьев и длины окружности).

Первый способ основан на применении для расчета планетарных и дифференциальных передач соотношений из главы 5, так как зубчатые колеса (кроме колеса 1) совершают плоскопараллельные движения. Особенно удобно для каждого из колес находить м.ц.с. и, как следствие, угловую скорость вращения колеса вокруг него. В качестве примера на рис.8.7 нанесены результаты такого расчета, выполненные для планетарной передачи, изображенной на рис.8.6. Угловая скорость 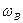кривошипа АВ и радиусы колес - известные величины.

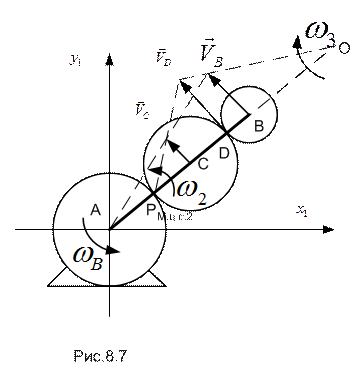
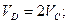
здесь 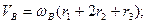Тогда: .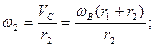

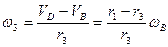При выводе формул учтено, что м.ц.с. колеса 2 находится в точке Р его контакта с неподвижным колесом 1, а м.ц.с. колеса 3 находится по известным скоростям двух его точек (D и B).

При расчете дифференциальной передачи вращение колеса 1 с заданной угловой скоростью 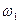приводит к необходимости найти положение м.ц.с. колеса 2 по известным скоростям двух его точек (С и P); положение м.ц.с. колеса 3 находится аналогично.

Другой способ расчета использует понятия сложного движения и называется методом остановки или методом Виллиса [2].

В этом случае движение каждого из колес передачи (планетарной или дифференциальной) представляется сложным, состоящим из относительного, по отношению к мысленно остановленному кривошипу АВ, и переносного – вместе с кривошипом АВ.

В качестве примера выполним расчет для дифференциальной передачи, изображенной на рис.8.8.а. Угловая скорость 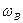кривошипа АВ, угловая скорость 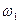колеса 1 и радиусы колес - известные величины.

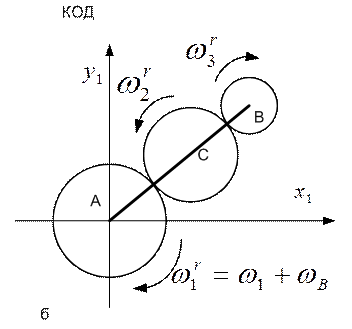
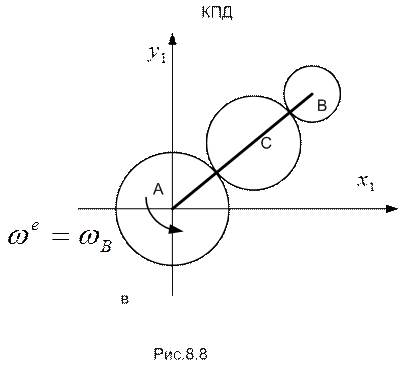
На рис.8.8.б изображена картина относительного движения (рядовая передача из трех колес; кинематика таких передач обсуждена в главе 4), а на рис.8.8.в – картина переносного движения (вращение кривошипа АВ и колес как единого целого вокруг точки А). В этом случае угловая скорость переносного вращения у всех колес одинакова и равна угловой скорости 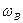кривошипа АВ, т.е. .

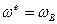Угловая скорость колеса 1 в его движении относительно кривошипа АВ будет , так как эти вращения происходят в разные стороны (вращение против хода часовой стрелки принято за положительное).

Угловая скорость колеса 2 в его движении относительно кривошипа АВ будет

.

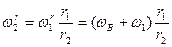Угловая скорость колеса 3 в его движении относительно кривошипа АВ будет

.

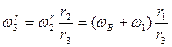Сложим угловые скорости составляющих движений с учетом направлений вращения:

; ;

.

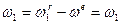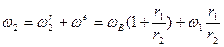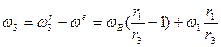Алгоритм расчета планетарной передачи тот же; при этом вследствие равенства нулю абсолютной угловой скорости колеса 1, угловая скорость вращения по отношению к кривошипу АВ будет равна угловой скорости кривошипа АВ и противоположно направлена, т.е. 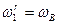; вращение против хода часовой стрелки принято за положительное.

Положив 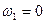в соотношениях, выведенных методом Виллиса, получим соотношения для планетарной передачи; эти соотношения совпадают результатами, полученными выше при использовании понятия м.ц.с. (что естественно).

8.6.Сложение поступательного и вращательного движений. Винтовое движение *

В главе 6 движение свободного твердого тела было представлено суммой переносного поступательного движения с кинематическими характеристиками точки, принятой за полюс, и относительного движения, являющегося сферическим движением тела относительно полюса. Там же было указано, как рассчитать кинематические характеристики любой его точки.

Возможна иная ситуация, когда тело движется поступательно относительно подвижной системы отсчета, совершающей вращательное движение. Если вращение происходит вокруг неподвижной оси, могут иметь место три случая.

1. Векторы 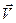и 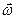перпендикулярны. Тогда справедливо утверждение, что любое сечение тела, образованное плоскостью, перпендикулярной оси вращения, остается в этой плоскости в течение всего движения. Такое движение было названо плоскопараллельным (см. главу 5).

2. Векторы 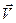и 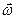параллельны. Выберем оси неподвижной (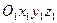) и связанной с телом Р (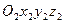) координатных систем так, чтобы их оси 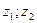были параллельны указанным векторам (рис.8.9).

Скорость произвольной точки М тела Р определяется выражением (7.10):

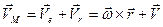, (8.9)

в котором относительная скорость 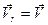параллельна оси 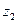, а переносная скорость перпендикулярна плоскости, проходящей через ось 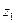и точку М. Анализ рис.8.9 показывает, что точка М будет двигаться по боковой поверхности кругового цилиндра с осью 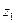и радиусом 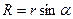. Такая траектория носит название винтовой линии.

Время одного оборота тела в винтовом движении определяется по формуле 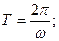шаг винтовой линии (изменение аппликаты точки М за время одного оборота)

.

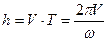Величина 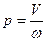называется параметром винта, а результирующее движение тела – кинематическим винтом.

3. Векторы 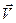и 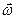образуют угол 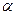. Разложим вектор 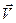на две составляющие так, чтобы 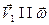, а 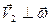. Теперь поступательное движение со скоростью 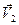заменим парой вращений (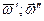). В полученной системе из четырех движений два последних эквивалентны покою. Исключив их из рассмотрения, получаем новое винтовое движение с кинематическими параметрами , при этом ось винта отстоит от оси 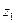на расстояние 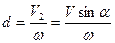, а шаг винта .

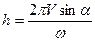9. Кинематика несвободной системы *

Date: 2015-09-03; view: 730; Нарушение авторских прав